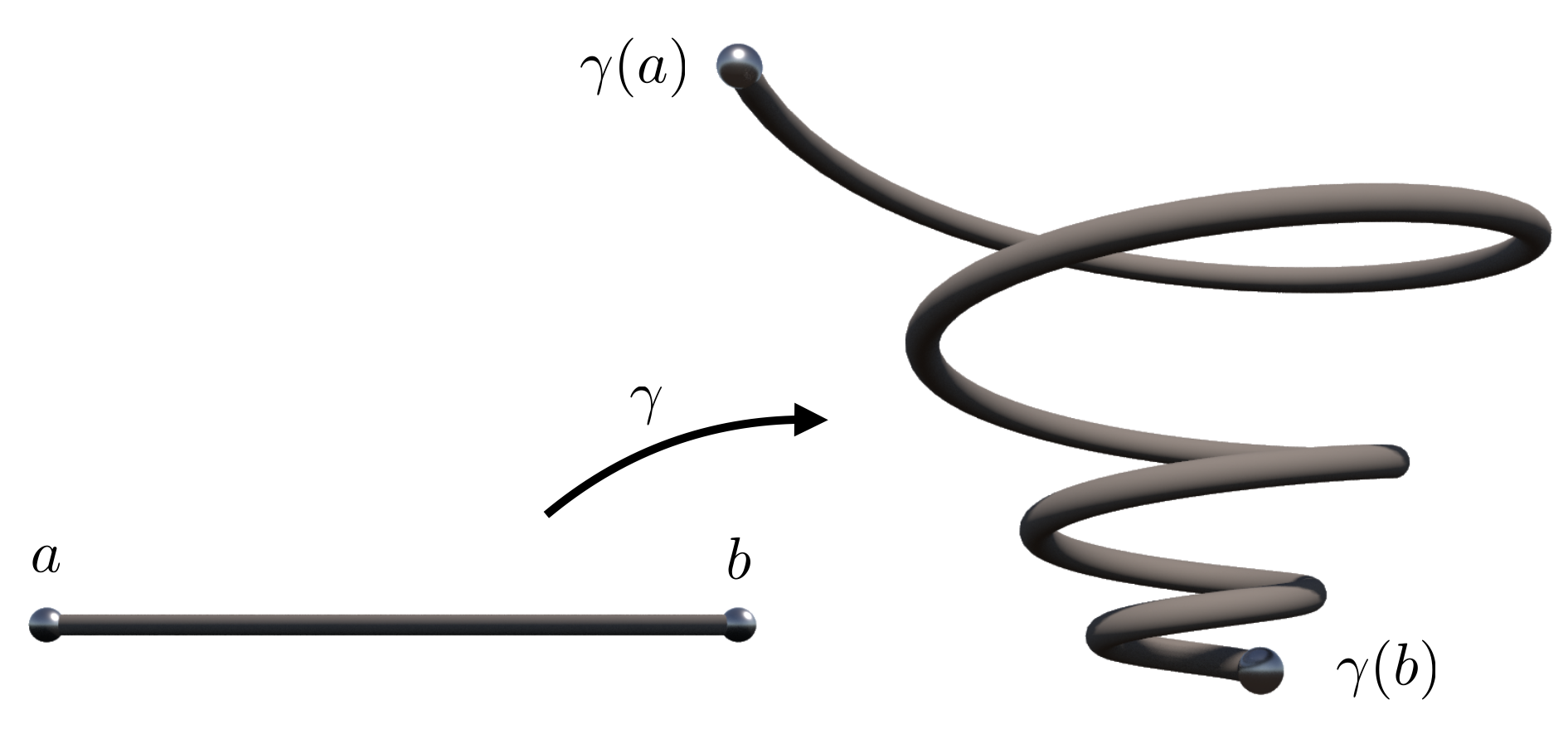
In most situations we will start with already existing geometry and transform it into new geometries. Such is the usual method to create curves from lines that we will now learn.
This approach is similar to the standard way of dealing with curves and surfaces in differential geometry: One starts with a parameter domain $M$ which could be a subset of $\mathbb{R}^n$ or just an abstract $n$-dimensional manifold. For concreteness, just imagine that $n$ is either one (for the study of curves) or two (for surfaces). The geometric objects of interest are then certain smooth maps $f:M \to \mathbb{R}^3$. Such an $f$ is then called a parametrized curve (in case $n=1$) or a parametrized surface (if $n=2$).
If $M$ is a compact connected one-dimensional manifold with non-empty boundary we can as well assume that $M$ is a closed interval $[a,b]$ on the real line:
Open Curves
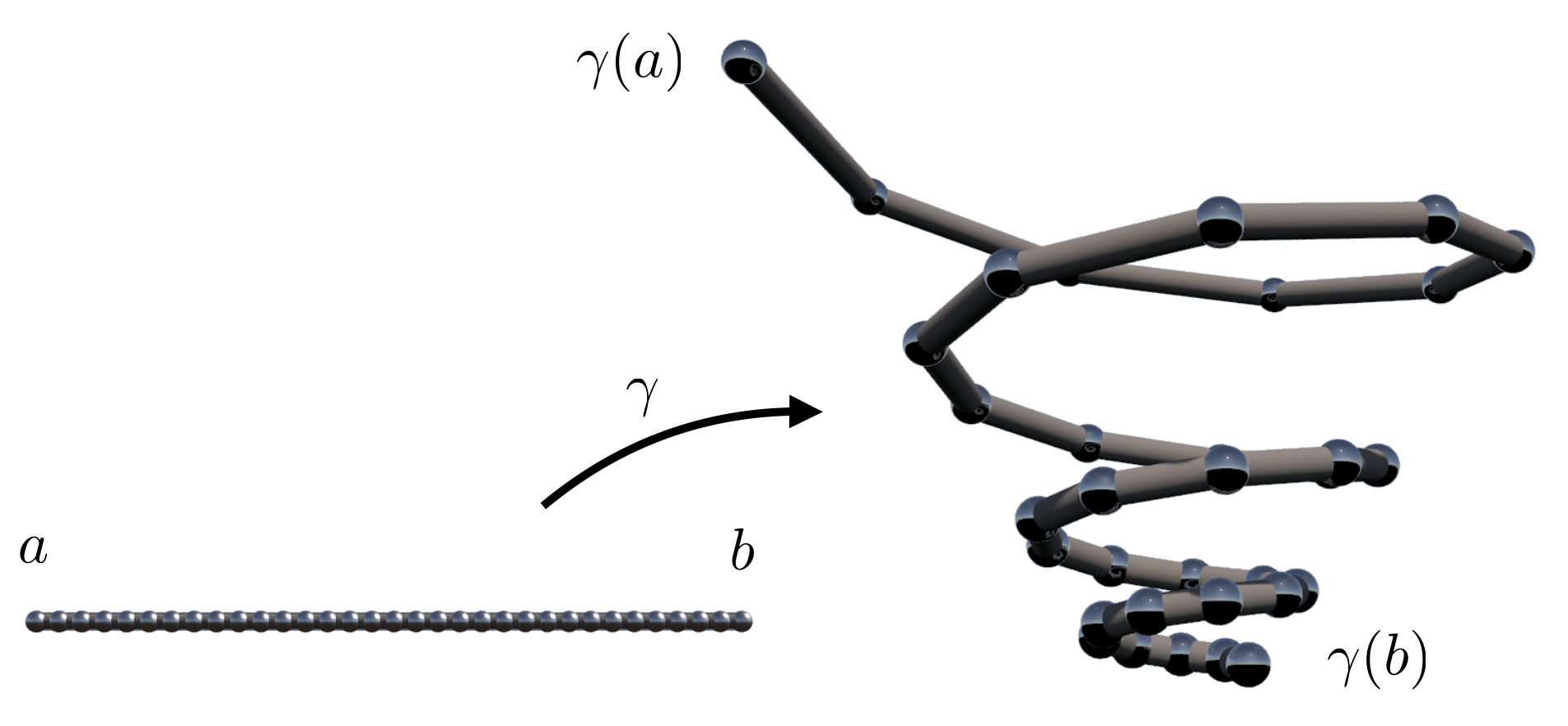
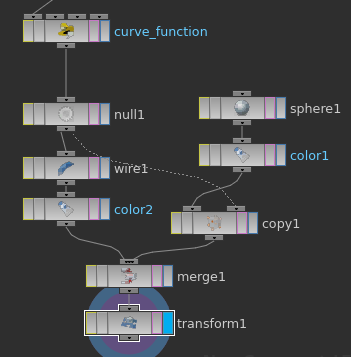
In Houdini a discrete version of the interval $[a,b]$ can conveniently supplied by a Grid node where the Rows has been set to one. The Columns parameter specifies the number of equally spaced sample points on interval. Instead of specifying $a,b$ directly we have to provide $b-a$ as the first component of the Size parameter and $(a+b)/2$ as the first component of the Center parameter. Afterwards we use a node of type Point Wrangle in order to map the $x$-coordinate to the desired space curve.
The curve in the last picture results from the VEX code below. alpha, omega and lambda are three float parameters of that Point Wrangle node.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#include "Math.h" float alpha = PI/180 * ch("alpha"); float omega = ch("omega"); float lambda = ch("lambda"); float t = @P.x; float c = cos(alpha); float s = sin(alpha); float r = exp(lambda * t); @P.z = r * s * cos(omega * t); @P.x = r * s * sin(omega * t); @P.y = r * c; |
Guided Example: Open Curve
Lets see in detail how we archived this. First create a grid node (we named it domain_grid) and adjust its size to 1,1 and the number of rows to 1 and the number of columns to however many points you want.
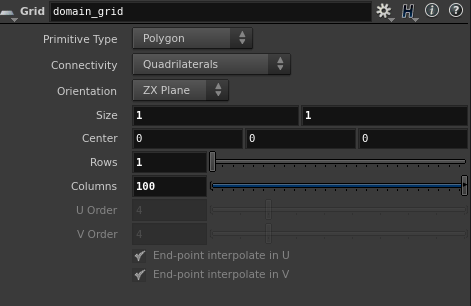
Now we have a curve that is just on the x-axis with values from -1 to 1, meaning that @P.x is the carrier of the running parameter and the only thing we care about. We can transform these values from the [-1,1] to the [0,1] interval using a point wrangler with the following code.

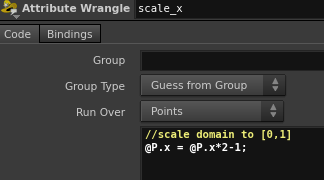
|
1 2 |
//scale domain to [0,1] @P.x = @P.x*2-1; |
Next we will add another point wrangler to take the @P.x values and use them in our function to map them.
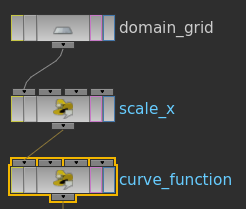
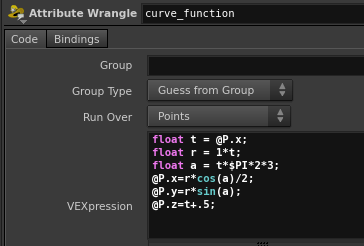
|
1 2 3 4 5 6 7 8 |
// compute the curve float t = @P.x; float r = 1*t; float a = t*$PI*2*3; // parametrize @P.x=r*cos(a)/2; @P.y=r*sin(a); @P.z=t+.5; |

Of course we advise to bring in the style nodes from previous tutorials.
Optional:
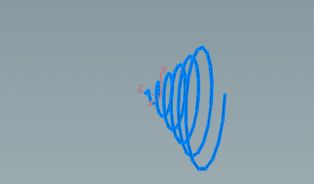
You can also add the @Time to @P.x in order to move along the parameter axis. We do this in the scale_x node.
|
1 2 3 |
//scale domain to [0,1] // we additionally animate the curve for fun @P.x = @P.x*2-1+ @Time/360*100; |
Closed Curves
If $M$ is a compact connected one-dimensional manifold without boundary then we can as well assume that $M$ is the unit circle $S^1\subset \mathbb{R}^2$:
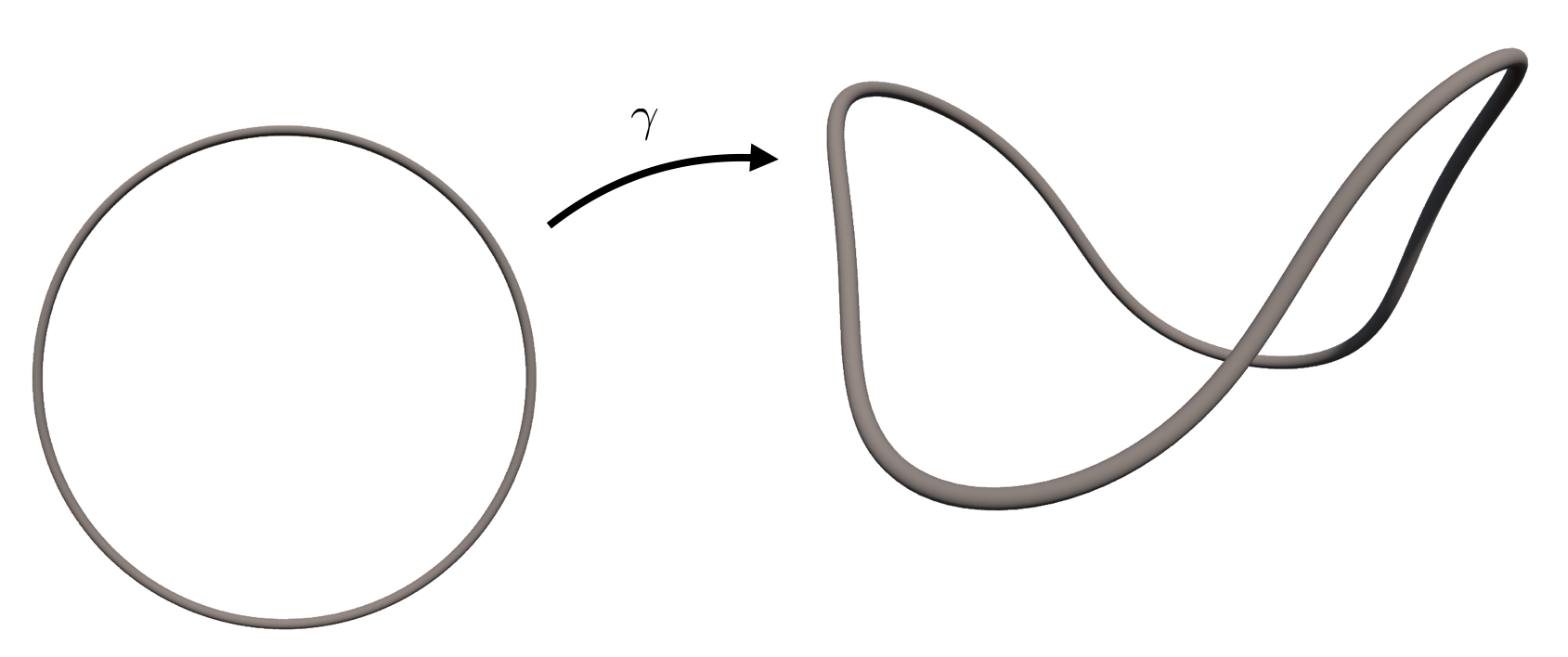
In Houdini a discrete version of the unit circle $S^1$ can conveniently be supplied by a Circle node where the Primitive Type has been set to Polygon. The Divisions parameter specifies the number of equally spaced sample points on the circle. Afterwards we use a node of type Point Wrangle in order to map the$(x,y)$-coordinates on the circle to the desired space curve. The curve in the last picture results from the VEX code below. k is an integer parameter and r a float parameter of that Point Wrangle node.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
#include "math.h" #include "$HIP/include/Complex.h" // we have written Complex.h our self. // It is located in the directior "include" next // to the Houdini file we are currently working with. // create parameters of our special arc-length curve float k = 5; float r = 1; float q = pow(r,2*k-1); float m = 2*k-1; float a = 1/(2*k-1); float b = 2*pow(r,k)/k; float fac = 1/(r+q); // read coordinates float c = @P.x; float s = @P.y; // interprete as complex number and take complex exponents vector2 zm = cpow(set(c,s),(int)m); vector2 zk = cpow(set(c,s),(int)k); // parametrize the curve @P.x = fac*(r*c + a*q*zm.x); @P.y = fac*b*zk.y; @P.z = fac*(r*s - a*q*zm.y); |
We have used here an include file “Complex.h” which implements some complex arithmetic function definitions. We discuss this in detail in the tutorial on Custom Code.

Note that the sample points on the space curve roughly look equally spaced. The reason is that in this particular example the corresponding smooth curve is parametrized by arclength for all values of the parameters $k,r$. This means that if $p$ runs through the unit circle with unit speed then also $\gamma(s)$ travels with unit speed.
Guided Example: Closed Curve
Open up your circle node and set the parameters as shown in the gif. Make sure that the Primitive Type is set to Polygon.
Continue by implementing two point wranglers with the VEX code below. The Time_Motion node is optional and implemented to show the closed nature of the curve.
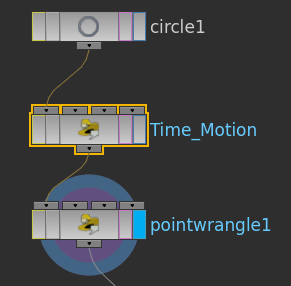
|
1 2 3 4 5 6 7 8 |
// read coordinates float c = @P.x; float s = @P.y; // read time float t = @Time/2; // parameterize with a time rotation @P.x = cos(t)*c +sin(t)*s; @P.y = -sin(t)*c +cos(t)*s; |
|
1 2 3 4 5 |
// here we transform our points on the circle to have // desired closed curve shape. float c = @P.x; float s = @P.y; @P.z = 0.1*sin(10*atan2(s,c)); |
Here we used atan2(s,c) in order to get the angle of the point in the circle.
Don’t be surprised if your resulting object is still not a curve. You will still only have a deformed circle. In order to make the function pretty again you need to insert the wire frame and spheres at least. Tip: always try to keep the nodes as organized as possible.
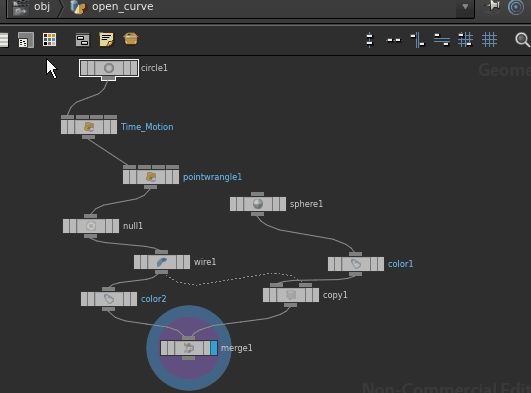
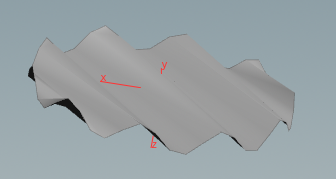
Optional note: By inserting a remesh node you can make use of the whole geometry. This might become handy if you need a triangulation of a disc.