The euclidean plane isometry consists of 5 motions:
- Identity
- Reflection
- Rotation
- Translation
- Glide Reflection
Suppose $G<E_2$ is a discrete group. First consider the translation subgroup of $G$. It holds $G\cap \mathbb{R}^2 < E_2$. We have
- $E_2 = \mathbb{R}^2 \rtimes O_2 $.
- $E_2 \overset{\varphi}{\longrightarrow} O_2$.
- $ker(\varphi) = \mathbb{R}^2 = $Translations.
- $ker(\varphi|_G)= G \cap \mathbb{R}^2$.
The discrete translation group forms a lattice of dimension $k= 0,1,2$.
$k=1:$ There are no translations in $G$. This implies that $G$ has a fixed point ($G$ has no glides). Thus $G<O_2$ is a finite subgroup $G=C_n$ or $D_n$ for some $n=1,2,3$. As groups of symmetries in $\mathbb{E}^2$ these are called the rosette groups or point groups since they leave at least one point fixed.
$G=C_n$ are called the cyclic group. 
The cup (first object) is $C_2$ since it has a $180^°$ symmetry. The recycling logo (2nd object) is $C_3$ and the star (3rd object) $C_5$ since the they are $120^°$ and $72^°$ symmetric. The group $C_1$ has no symmetry and can be represented by an L or an R.
$G=D_n$ are called the dihedral group.
Starting with the upper left the square is $D_4$, the rhombus is $D_2$ the triangle $D_1$. The dihedral group is the group of regular polygons, so an n-gon is $D_n$.
$k=1:$ These groups are called the frieze groups. They have the following definition:
$G\cap \mathbb{R}^2 = \{ \tau_{nv} : v\neq 0 \in \mathbb{R}^2, n\in\mathbb{Z} \} = \langle \tau_v\rangle\cong \mathbb{Z}$.
$k=2:$ These groups are called the wallpaper groups. They have the following definition:
$G\cap \mathbb{R}^2 = \langle \tau_v, \tau_w\rangle \{ \tau_{nv+mw} : v,w\neq 0 \in \mathbb{R}^2, n,m\in\mathbb{Z} \} \cong \mathbb{Z}^2$.
There are seven distinct subgroups (up to scaling and shifting of patterns) in the discrete frieze group generated by a translation, reflection (along the same axis) and a 180° rotation. An overview gives the following picture 
The Orbifold notation was the name we used in the lecture.
Take a width-$n$ strip $[0,n]\times\mathbb{R}\subset\mathbb{R}$ and glue its edges to give a cylinder. Any of our seven groups will give a group symmetry of the cylinder with exactly $n$-fold rotation around vertical axis. This gives $7$ families of symmetry groups, indexed by $n$. These are finite subgroups of $O_3$. They are exactly the ones that preserve the equator (or equivalent preserve the poles). These are called the axial groups:
- $nn$, rotations (abstr: $\mathbb{Z}_n$)
- $nx$, rotary directions (abstr: $\mathbb{Z}_{2n}$)
- $n*$, (abstr: $\mathbb{Z}_n \times \mathbb{Z}_2$)
- $*nn$, (abstr: $D_n$)
- $22n$, (abstr: $D_n$)
- $2*n$, (abstr: $D_{2n}$)
- $*22n$, ($D_n \times \mathbb{Z}_2$)
Special cases for $n=2$:
- $22$, a 2-fold rotation (abstr: $\mathbb{Z}_2$)
- $2X$, a 4-fold rotary reflection (abstr: $\mathbb{Z}_4$)
- $2*$, rotation, mirror, and antipodal map (abstr: $\mathbb{Z}_2^2$)
- $*22$, 2 mirrors which yield a rotation (abstr: $\mathbb{Z}_2^2$)
- $222$, rotations (abstr: $\mathbb{Z}_2^2$), the Klein-4-group
- $2*2$, rotation and mirror, (abstr: $D_4$)
- $*222$ only reflections, (abstr: $\mathbb{Z}_2^3$)
Note that the abstract groups sometimes look different as, e.g., for the group $222$, which should have $D_2$ as its abstract group instead of $\mathbb{Z}_2$. These are equivalent because
$D_{2} \cong D_1 \times \mathbb{Z}_2 \cong \mathbb{Z}_2$.
In general, for odd $m \in \mathbb{N}$, it holds
$D_{2m} \cong D_{m} \times \mathbb{Z}_2$, and $\mathbb{Z}_{2m} \cong \mathbb{Z}_m \times \mathbb{Z}_2$.
For $n=1$, only three different groups remain:
- $11 = 1$, the trivial group
- $1x = x$, identity and antipodal map (abstr: $\mathbb{Z}_2$)
- $1* = * = *11$, a single mirror, (abstr: $\mathbb{Z}_2$)
Of course, there are more discrete subgroups of $O_3$. Most of them correspond to the symmetry groups of the platonic solids. First, we give the theorem:
Theorem: The finite subgroups of $O_3$ are the 7 families of axial groups and the 7 platonic symmetry groups $*235$, $235$ (symmetries of icosahedron and its dual, the dodecahedron), $*234$, $234$ (symmetries of the cube and the dodecahedron), $*233$, $233$ (tetrahedron), and $3*2$ (the so-called pyritohedral symmetry).

The figure on the left shows the icosahedron inside of a dodecahedron. Recall that the dual or reciprocal of a solid evolves from faces becoming vertices, roughly speaking. A symmetry of one solid is also a symmetry of its dual.
The symmetry group is $*235$, which has the rotation part $235$ as subgroup. (http://apollonius.math.nthu.edu.tw/d1/dg-07-exe/943251/dynamic/duality.htm)
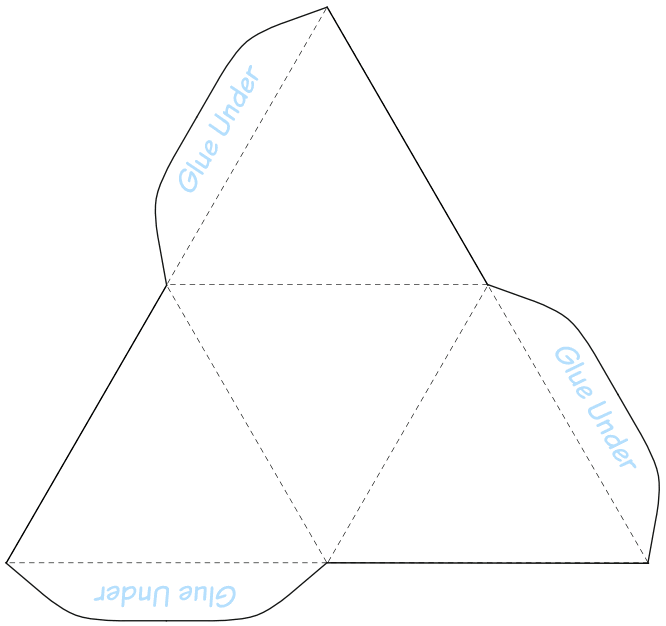 The tetrahedron has the symmetry group $*233$, with rotation subgroup $233$.
The tetrahedron has the symmetry group $*233$, with rotation subgroup $233$.
You can easily make a tetrahedron yourself by using the figure to the right, and search for the symmetry groups yourself.
Note that the tetrahedron is dual to itself.
The cube and its dual counterpart, the octahedron, have the symmetry group $*234$, and $234$. The last symmetry group, the pyritohedral symmetry group, comes as the intersection of the octahedral and the dodecahedral symmetry groups,
$3*2 = *235 \cap *234$.
In the figure below, you see a pyritohedron, which is not platonic (note that the faces are irregular pentagons).

Wallpaper groups
Back to $E_2$ (the euclidean motions in the plane), the discrete subgroups which have a translational part of dimension 2 are called wallpaper groups. In the figure below, you find an exhaustive list of the 17 wallpaper groups, each with its fundamental domain, and generating symmetries.

