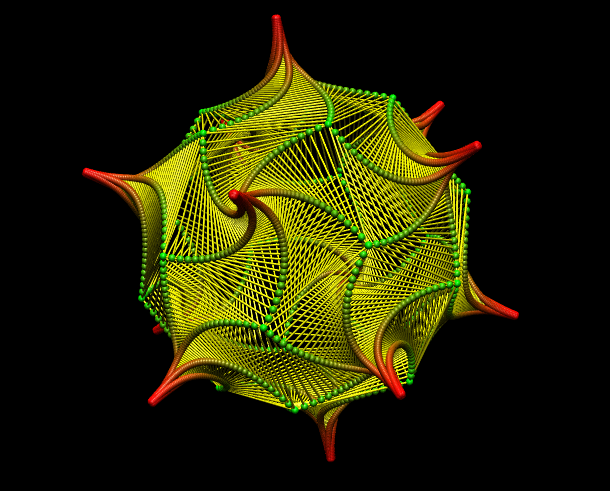
Today in class I presented a project which I have been working on, on and off, for several years. It is a visualization of the Schatz linkage. You can access the webstart I showed here. The video I showed at the beginning of the class can be seen here. The pictures of the wooden oloid which Thomas Neukirchner made can be found here. Thomas’s diagrams and plywood models of the oloid can be found here. The latest edition of Paul Schatz’s book Die Welt ist Umstülpbar: Rhythmusforschung und Technik can be found here on Amazon. If you are interested in this theme then mark your calender for April 4-6, when there will be a weekend event in Berlin devoted to themes related to Paul Schatz’s research. A few more details can be found here.
On Thursday, Jan. 9, we will take some time to evaluate this “project presentation” in regard to the various criteria mentioned in the evaluation handout. Be there or be square! I will also discuss the half-edge data structure and demonstrate some advanced features of the discretegroup package, and, if time permits, more!
Assignment 6: As discussed in class on our final meeting before the holidays, the next assignment is not a programming assignment but rather a planning assignment. I ask you to enter a description of your project as a comment to this blog post. Use the account name studentmv with the clever password. Please sign your comment with either your name(s) or with your student number(s). Your comments are due as usual on Friday at midnight. (That’s Friday Jan. 10). The details of the description are provided below, but first comes a “news flash” regarding a change in the way property files are handled in the basic template.Assignment class.
Improved way to provide property files. Although I didn’t do much work over the holiday break, I did play around some with webstarts — enough to realize that the current way that property files are handled doesn’t work with webstart technology. So I’ve figured out a new way to handle property files that does work with webstarts, and has other advantages. Here’s how it works:
- If you have a class named MyAssignment.java that inherits from template.Assignment, then store off the properties in a file named myAssignment.xml (note the leading lower case letter!) in the same folder as MyAssignment.java. Implement the method getPropertiesFile() to return null. Or, remove your implementation of the method, it’s no longer an abstract method and by default it returns null.
- That’s all you have to do. Now your class should read the property file correctly whether run “normally” or as a webstart application (which your project application will ultimately need to do).
- Please try this out to make sure it works for you — if you don’t change anything the old code will continue to work but you should get used to using the new approach.
What to include in your description.
- Mathematics. The description should begin with the mathematical content of the project. Try to be as precise and accurate. Zoom in gently — make clear to which domain of mathematics this content belongs. Use technical language if necessary to specify this. If possible, include one or two references (either articles or books) which provide a more detailed description of the context of your project. None of the projects exists “in a vacuum”, give a pointer to your point(s) of departure.
- Software design. Begin this section by a statement describing the concrete goal of your project. For example, “We intend to create an application to allow the user to explore the 3-dimensional kaleidoscopes introduced above [in the mathematical section].” Describe then the software tools and building blocks you think you will need in order to realize this aim, and how they will be put together. For example, building blocks might include “jReality geometry factories, the de.jtem.halfedge package, and the de.jtem.discretegroup package”; additionally indicate which parts of these building blocks you will use and how they will be combined. Think if this as the blueprint for your project. Of course at this stage of the planning it shouldn’t be too detailed.
- User experience. Finally, briefly indicate how you envision a typical “usage cycle” of your program. What choices does the user have, how can he/she interact with the software sketched in the previous section? Can the user save the state of the program from one invocation to the next? Will you rely on sliders and dials, or have you ideas for innovative interactive tools? Will your application be particularly aimed at the PORTAL? Will there be a connection to 3D printing?