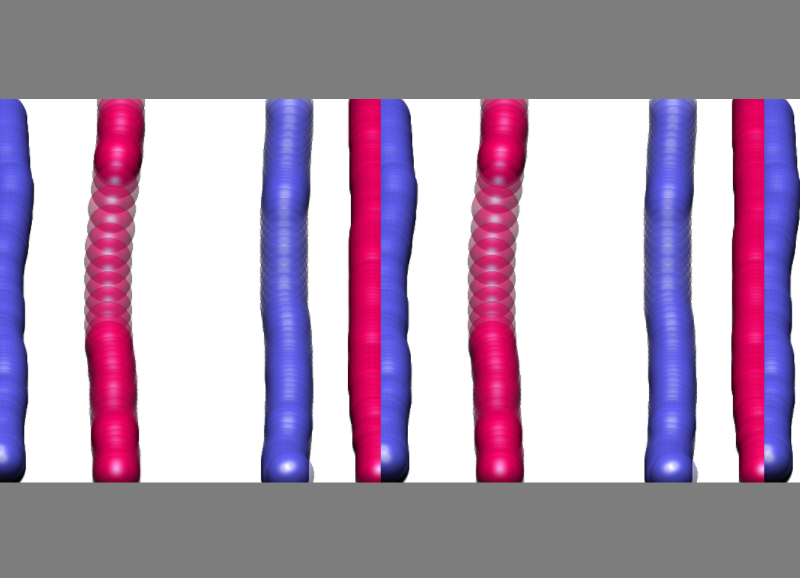
Assignment5: For the class’s Christmas calendar, each group is asked to contribute one beautiful, self-made mathematical image. Please subclass the java class template.Assignment to produce an application named Assignment5 which displays this image when it is run. I encourage you to use this assignment as a preparation for your project — even if you don’t know what the topic of your project is! Choose some favorite domain of mathematics and use what you’ve learned about jReality to create an image appropriate for inclusion in a Christmas calendar. For example, the image below shows another of my free-lance efforts for Matheon from several Christmases ago … Assignment5 due on Dec 6 13 — see the next paragraph for the continuation of Assignment4, due on Dec. 6.  Assignment4 continuation. I have, as promised, extended Assignment 4 to include another “assignment”. The problem with the standard painting algorithm is shown in the following image: when the center of the brush approaches the boundary of the fundamental region (always a square for these groups), it can happen that only part of the brush is painted. See the red and blue “half-paths” which join along a seam: the red was painted with the center of the brush slightly to the left side, the blue with the center of the brush just slightly to the right. It ain’t right — you gotta fix it.
Assignment4 continuation. I have, as promised, extended Assignment 4 to include another “assignment”. The problem with the standard painting algorithm is shown in the following image: when the center of the brush approaches the boundary of the fundamental region (always a square for these groups), it can happen that only part of the brush is painted. See the red and blue “half-paths” which join along a seam: the red was painted with the center of the brush slightly to the left side, the blue with the center of the brush just slightly to the right. It ain’t right — you gotta fix it.
To complete this assignment: Please make sure your Assignment4 class subclasses from template.AbstractAssignment4 not from a copy in your student package. Then update to the latest version of my repository. You should only need to make a copy of template.Assignment4PaintTool — see the directions at the top of this file. The new version of AbstractAssignment4 invokes this class to provide painting support — your task is to edit Assignment4PaintTool so it supports all 7 frieze groups so that no seams are visible during painting. This assignment is due in a week, on Dec. 6.
Note: Do some of your frieze groups appear wrong (the last three groups on the menu, when there should be two rows there is only one with L’s lying on top of each other)? If so, make sure that the updateCopies() method in Assignment4 contains the following line of code:
MatrixBuilder.euclidean().
translate(0, (whichGroup >= 4 && whichGroup <= 6) ? .5 : 0, 0).
assignTo(fundamentalDomain);It could be that you made a copy of template.Assignment4Example before I included the above line of code.
Mathematical News. This week we continue the exploration of planar (or at least 2-dimensional) symmetry patterns. The focus turned from frieze groups to spherical groups, that is, groups of isometries of the 2-dimensional sphere $\mathbf{S}^2$. This is just the familiar orthogonal group $O(3)$, and a point group is a discrete subgroup. Recall a discrete subgroup is one in which the identity element is isolated, there is no sequence of group elements converging to it.
Fundamental domains and quotient spaces. Before continuing the investigation of particular groups, Mr. Gunn introduced some general language. First he observed that we are considering symmetries of 2-dimensional spaces of constant curvature, such as the Euclidean plane or the 2-sphere. In general we call this space $\mathbf{X}$. And a discrete group of motions will be in general denoted as $\Gamma$. He then discussed the concept of a fundamental domain for $\Gamma$. That is a subset $D \subset \mathbf{X}$ such that $\cup_{g\in D}{g(D)} = \mathbf{X}$ and $g_1(D) \cap g_2(d) = \emptyset$ for $g_1, g_2 \in \Gamma$. That is, the copies of $D$ cover $X$ without overlap. Such a covering is called a tessellation – in German, Pflasterung. We can arrive at the same concept more abstractly by defining an equivalence relationship on $\mathbf{X}$: \[ \mathbf{P} \sim \mathbf{Q} \iff \exists g \in \Gamma ~\text{such that}~ g(\mathbf{P}) = \mathbf{Q} \] The set of equivalence classes is called the quotient of $\mathbf{X}$ by $\Gamma$ and is written $\mathbf{X}/\Gamma$. We want to understand better how such quotient spaces behave.
Simplest example: the circle as quotient of the line. Mr. Gunn explained in detail the construction of the quotient space $\mathbf{E}^1/ \{ t \}$ where $ \{ t \}$ is the discrete group generated by the unit translation $t: x \rightarrow x+1$. He showed that $\mathbf{E}^1/ \{ t \}$ is a circle $S^1$ by twisting the line into an infinite helix so that the orbit of any point under the group lies on the vertical line passing through it. Then, by looking down on this helix from far away, each vertical line collapses to a point and we are left with a circle.
Connection of quotient space and fundamental region. The quotient space is closely related to a fundamental domain. A fundamental domain for this group is the half-open interval $[0, 1)$; the quotient space is obtained by taking into account the fact that $0 \sim 1$, hence we have to “glue” the two ends of the segment together to obtain the quotient space. In short, the quotient space can be obtained from a fundamental region by remembering to glue together parts of the boundary of the FD which are identified under some group element.
Dirichlet domain. There are many possible choices for a fundamental domain. For the groups we consider, we can always arrange that the fundamental domain is topologically an open disk along with a subset of its boundary.
The problem with overlaps. An n-dimensional euclidean manifold is a space in which every point has a neighborhood homeomorphic to $\mathbf{R}^n$. When is the quotient space a manifold? Define the stabilizer of a point P to be the set of group elements which fix P: $s(P) := \{g \in \Gamma \mid g(P) = P\}$. Since $\Gamma$ is discrete, $s(P)$ is finite. It is exactly points with non-trivial stabilizers that cause overlaps in the tessellation. It’s easy to see that copies of any fundamental region will “overlap” at such points. For let $D$ be a fundamental domain$g, h \in s(P), P \in D$. Then $f(D) \cap g(D) = f(P) \neq \emptyset$. On the other hand, if $s(P) = \{id\}$ for all $P\in D$, then the action is called fixed-point free and the resulting quotient is a manifold. This is equivalent to saying we can find a fundamental region whose copies cover $\mathbf{X}$ without overlap. This is the case for example for the translation frieze group $\infty \infty$ or the group generated by one glide reflection $\infty X$.
Orbifolds to the rescue. If $s(P)$ is not the trivial group, the quotient space $\mathbf{X}/\Gamma$ in a neighborhood of $P$ will not look like $\mathbb{R}^n$ but rather like the quotient $\mathbb{R}^n/s(P)$. An orbifold is defined similarly to a manifold, with the looser requirement that each point $P$ has a neighborhood homeomorphic to $\mathbb{R}^n/G$ for a finite group $G$. In effect, we “split” the point into $k$ identical “fractional” parts (where $k = | s(P) | $) so that the $k$ “overlapping” copies of $P$ (each of size “$\dfrac1k$”) together “add up” to a single point. In this way we can rescue the statement “The copies of D cover $\mathbf{X}$ without overlap.”
Example. Consider a rotation of order-2 in the plane and the associated cyclic group $C_2$. The rotation center $P$ is fixed by the both the identity and the rotation, so is not trivial. In a neighborhood of $P$, $\mathbf{E}^2/C_2$ looks like a cone formed by rolling a straight angle at $P$. [need to show a picture to explain this].
Why this is important. This relation between symmetry groups and quotient spaces is important since it turns out that every topological space can be realized in this way as the quotient of some simply-connected space by an appropriate discrete group. More on this on Thursday when I’ll show the video “Shape of Space”. This wasn’t completely proven until the Poincare Conjecture was proved by Grigori Perelman in 2006.
The spherical groups fixing two points. We began by restricting attention to symmetry groups which fix two antipodal points. We began by showing that there are a family of cyclic groups generated by a rotation of order $n$, fixing the north and south pole and rotating along the equator, so to speak. One sees easily that fundamental domain for this group is a two-sided section of the sphere extending from north to south pole, whose one side is mapped to the other side by the rotation. This region is called a bigon since it has two sides and two vertices. Since the angle at each vertex is $\dfrac{2 \pi}{n}$, the group is called $nn$. … to be continued … In the meantime see this Wikipedia article.

Pingback: 9.12 Assignment5 | Mathematical Visualization
Pingback: Course Log | Mathematical Visualization