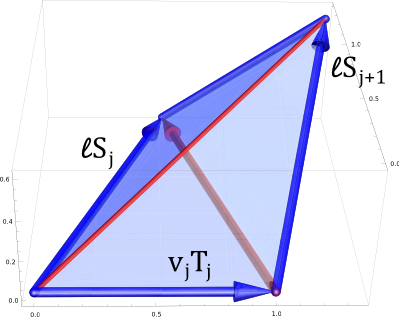
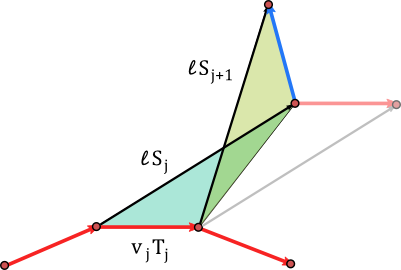
Let $\gamma_1,\ldots,\gamma_n\in \mathbb{R}^3$ be a regular discrete space curve. We are looking for another discrete space curve $\tilde{\gamma}$ that satisfies the first two conditions we had in the planar case: The distance between corresponding points $|\tilde{\gamma}_j-\gamma_j|$ is a constant $\ell$ and corresponding edges of $\gamma$ and $\tilde{\gamma}$ have the same length. Then (with a notation as in the previous post) we see that compared two the planar case we have a whole one-parameter family of possible choices for $S_{j+1}$: The vector $S_{j+1}$ can be the result of rotating $S_j$ around $\ell S_j + v_j T_j$ by any chosen angle.

One can imagine to start with a parallelogram with sides $v_j T_j$ and $\ell S_j$. The parallelogram is then folded around the diagonal whose direction is $\ell S_j-v_jT_j$.

Folding by 180 degrees corresponds to the Darboux-transformations we studied in the two-dimensional setting. It is given by the map

\[y\mapsto (\ell S_j-v_jT_j)y(\ell S_j-v_jT_j)^{-1}.\]

Any other folding angle (except for angle zero that would leave us with the parallelogram) can be realized as

\[y \mapsto qyq^{-1}\]

with $q$ of the form

\[q=r+\ell S_j-v_jT_j.\]

Here $r$ is an arbitrary real number. This leads to

\[S_{j+1}=(r+\ell S_j-v_jT_j)S_j(r+\ell S_j-v_jT_j)^{-1}\].

Definition: A discrete space curve $\tilde{\gamma}$ is called a Darboux transform of $\gamma$ with rod length $\ell$ and twist $r$ if

\[\gamma_j=\gamma_j+\ell S_j\]

and $S_1,\ldots, S_n$ satisfy the above equation.

Let us omit the subscript $j$ and use a subscript “+” instead of $j+1$. Combining then in the above formula the $S$ in the middle with the left bracket we see that the map $S\mapsto S_+$ is fractional linear:

\[S_+=((r -v T) S-\ell)((r -vT)+\ell S)^{-1}.\]

To investigate this map further we write $S$ as the stereographic projection with center $-T$ of some point $Z\in \mathbb{R}^3$ orthogonal to $T$:

\begin{align*} S &=(1-ZT)T(1-ZT)^{-1} \\\\ &=(T+Z)(1-ZT)^{-1} \\\\ &= T(1-ZT)(1+ZT)^{-1}.\end{align*}

The first line shows that $S\in S^2$ for $Z\perp T$. The second line shows that $Z\mapsto S$ is fractional linear. The last line shows that $S=Z$ in case $|Z|=1$. Let us plug this into the last formula for $S_+$:

\begin{align*}S_+&= ((r-vT)(T+Z)-\ell (1-ZT)((r-vT)(1-ZT)+\ell(T+Z))^{-1} \\\\ &=(((v-\ell)+rT)+(r-(v+\ell)T)Z)((r+(\ell-v)T)+((\ell+v)+rT)Z)^{-1} \\\\ &= \left(T+Z\frac{(\ell+v)-rT}{(\ell-v)-rT}\right)\left(1+TZ\frac{(\ell+v)-rT}{(\ell-v)-rT}\right)^{-1}.\end{align*}

Here the fractional notation is justified because the quaternions involved all commute. Thus in terms of the sterographic coordinate $Z$ the transition from $S$ to $S_+$ is just multiplication

\[Z+=MZ=Z\overline{M}\]

by a quaternion

\[M = \frac{(\ell+v)+rT}{(\ell-v)+rT}.\]

In the case $r=0$ this is in perfect accordance with the results of an earlier post.

As in the last post let $\gamma$ be a discrete curve in the $\mathbb{C}$ and $\tilde{\gamma}= \gamma+ \ell S$ be a Darboux transformation. Denote by $\alpha_j$ and $\beta_j$ the angles from the edges $T_J$ of $\gamma$ to the rod directions $S_j$ and $S_{j+1} respectively. Then

\begin{align*}S_j &= e^{i \alpha_j} T_j \\\\ S_{j+1}&= e^{i \beta_j} T_j.\end{align*}

We know that $S$ satisfies

\[ S_{j+1}=\frac{\ell S_j- v_j T_j}{\ell-v_j \bar{T}_j S_j}.\]

This yields

\[ e^{i\beta_j}=\frac{\ell e^{i\alpha_j}- v_j}{\ell-v_j e^{i\alpha_j}}.\]

Using the formula

\[e^{i\alpha}=\frac{1+it}{1-it}\]

where

\[t:=\tan \frac{\alpha}{2}\]

we then have

\begin{align*} e^{i\beta_j}&=\left(\ell \frac{1+it_j}{1-it_j}- v_j \right) \left(\ell-v_j \frac{1+it_j}{1-it_j} \right)^{-1} \\\\ &=\left(\frac{(\ell -v_j)+(\ell +v_j)it_j}{1-it_j}\right) \left( \frac{(\ell-v_j )-(\ell+v_j )it_j}{1-it_j} \right)^{-1} \\\\ &= \frac{1+i \mu_j t_j}{1-i \mu_j t_j} \,.\end{align*}

where

\[ \mu_j= \frac{\ell+v_j}{\ell-v_j}.\]

From this we conclude

\[\tan \frac{\beta_j}{2}=\mu_j \tan \frac{\alpha_j}{2}.\]

With the notation

\begin{align*}t_j&:=\tan \frac{\alpha_j}{2}\\\\ \tau_j&:=\tan \frac{\kappa_j}{2}\end{align*}

we obtain

\begin{align*}\tau_j&=\tan \frac{\beta_{j-1}-\alpha_j}{2}\\\\ &= \frac{\mu_{j-1} t_{j-1}-t_j}{1+\mu_{j-1} t_{j-1} t_j}.\end{align*}

The corresponding quantities for the Darboux transform $\tilde{\gamma}$ are

\begin{align*}\tilde{\alpha}_j &=\pi-\beta_j \\\\ \tilde{\beta}_j &= \pi- \alpha_j \\\\ \tilde{\tau}_j&=\tan \frac{\beta_j-\alpha_{j-1}}{2}\\\\ &= \frac{\mu_j t_j-t_{j-1}}{1+\mu_j t_j t_{j-1}}.\end{align*}

Note that we arrive at $\tilde{\tau}_j$ starting from $\tau_j$ if we interchange the roles of $t_{j-1}$ and $t_j$ and replace $\mu_{j-1}$ by $\mu_j$. If we apply this rule to

\begin{align*}1+\tau_j^2 &= \frac{(1+2\mu_{j-1} t_{j-1} t_j +\mu_{j-1}^2 t_{j-1}^2 t_j^2) + (t_j^2 -2 \mu_{j-1} t_{j-1} t_j +\mu_{j-1}^2 t_{j-1}^2)}{(1+\mu_{j-1} t_{j-1} t_j)^2} \\\\ &= \frac{(1+t_j^2)(1+\mu_{j-1}^2 t_{j-1}^2)}{(1+\mu_{j-1} t_{j-1} t_j)^2} \end{align*}

we obtain

\[1+\tilde{\tau}_j^2=\frac{(1+t_{j-1}^2)(1+\mu_j^2 t_j^2)}{(1+\mu_j t_j t_{j-1})^2}\]

Now the following is easy to prove:

Theorem: If $\gamma$ is a closed polygon in $\mathbb{R}^2$ with equal edge lengths and $\tilde{\gamma}$ is a closed Darboux transform of $\gamma$ then

\[\prod_{j=1}^n (1+\tau^2) = \prod_{j=1}^n (1+\tilde{\tau}^2).\]

We can interpret this as follows: The bending energy

\[\sum_{j=1}^n \log (1+\tau_j^2)=-\sum_{j=1}^n \log (1+\cos \kappa_j)\]

is the same for $\gamma$ and $\tilde{\gamma}$.

In this post we will work with a fixed sequence of lengths  $\ell_1,\dots,\ell_n>0$. This means we imagine polygons as composed of rigid edges connected by flexible joints at the vertices. Denote by $\mathcal{M}_m$ the space of curvature functions $\kappa=(\kappa_1,\ldots,\kappa_n)$ that correspond to closed regular polygons with $n$ vertices and tangent winding number $m$.  We can conveniently describe $\mathcal{M}_m$ as the zero set of the function

\begin{align*}\qquad F:(-\pi,\pi)^n &\to \mathbb{R}^3 = \mathbb{R}\times \mathbb{C}\\\\ F(\kappa_1,\ldots,\kappa_n)&=\left(\begin{array}{c} \kappa_1+\ldots +\kappa_n -2 \pi n \\  \ell_0 e^{i\alpha_0}+\ldots +\ell_{n-1}\, e^{i\alpha_{n-1}}\end{array}\right).\end{align*}

By the above calculation the derivative of $F$ is given as

\[F'(\kappa_1,\ldots,\kappa_n)\left(\begin{array}{c}\dot{\kappa}_1\\ \vdots \\ \dot{\kappa}_n\end{array}\right)=\left(\begin{array}{c} \dot{\kappa}_1+\ldots +\dot{\kappa}_n \\ \dot{\kappa}_1 \gamma_1+\ldots + \dot{\kappa}_n \gamma_n \end{array}\right).\]

Theorem: The rank of $F’$ is three at all points of $\mathcal{M}_m$. Therefore, by the implicit function theorem, $\mathcal{M}_m$ is a smooth manifold.

Proof: At a point $(\kappa_1,\ldots,\kappa_n)$ where the columns of $dF(\kappa_1,\ldots,\kappa_n)$ were linearly dependent we would have $a,b,c\in \mathbb{R}$ such that

\[a \mbox{Re}(\gamma_j)+b \mbox{Im}(\gamma_j)+c=0\]

for all $j$. But this means that the whole polygon lies on a straight line, which is impossible for a regular polygon.

$\square$

Suppose we have a vector field tangent to $\mathcal{M}_m$ that we want to follow numerically. This means that for any $\kappa=(\kappa_1,\ldots,\kappa_n)\in \mathcal{M}_m$  we are given a certain tangent vector

\[X_\kappa \in T_\kappa \mathcal{M}_m=\mbox{ker}F'(\kappa).\]

We want to find curves $t\mapsto \eta(t)\in \mathcal{M}_m$ that satisfy for all $t$

\[\dot{\eta}(t)=X_\eta(t).\]

If we already have constructed $\kappa=\eta(t)$ we might attempt to find $\eta(t+\epsilon)$ as

\[\tilde{\kappa}=\kappa+\epsilon \dot{\kappa}\]

where $\dot{\kappa}=X_{\kappa(t)}$. Since $\dot{\kappa}$ lies in the kernel of $F'(\kappa)$ the condition

\[\tilde{\kappa}_1+\ldots+\tilde{\kappa}_n=2\pi m\]

will be satisfied. The second condition

\[\ell_0 e^{i\tilde{\alpha}_0}+\ldots +\ell_{n-1} \,e^{i\tilde{\alpha}_{n-1}}\]

however is non-linear and so we cannot be sure that $\tilde{\kappa}$ corresponds to a closed regular polygon. We first have to project $\tilde{\kappa}$ back to $\mathcal{M}_m$.

To this end we add to $\tilde{\kappa}$ an element of $(T_\kappa\mathcal{M}_m)^\perp$, the normal space to $\mathcal{M}_m$ at the point $\kappa$. This space is spanned by

\begin{align*}N_0&=(1,\ldots,1)\\\\ N_1&=(x_1,\ldots,x_n) \\\\ N_2 &=(y_1,\ldots,y_n)\end{align*}

Here $\gamma_j=x_j+iy_j$ and we assume that a translation has been applied to $\gamma$ in order to achieve

\[\gamma_1+\ldots,+\gamma_n=0.\]

Since the condition $\tilde{\kappa}_1+\ldots+\tilde{\kappa}_n=2\pi m$ already has been dealt with there is no need to work with $N_1$. We therefore are looking for $\lambda_1,\lambda_2 \in \mathbb{R}$ such that

\[f(\lambda_1,\lambda_2)=(0,0).\]

Here

\[f(\lambda_1,\lambda_2)=G(\kappa+\lambda_1 N_1 + \lambda_2 N_2)\]

where

\[G(\hat{\kappa}):=\ell_1e^{i\hat{\alpha}_1}+\ldots+\ell_{n-1}e^{i\hat{\alpha}_{n-1}}\,.\]

Thus we are left with the problem of finding a zero of $f$. From the calculation at the beginning of the post we know the derivative of $f$, so a Newton method seems the right thing to implement.

The moduli space (meaning congruent polygons are considered as equal) of open regular polygons $\gamma_0,\ldots,\gamma_n$ in the plane can be parametrized by parameters

\[(\ell_0,\ldots,\ell_{n-1},\kappa_1,\ldots,\kappa_{n-1})\in (0,\infty)^{n-1} \times (-\pi,\pi)^{n-2}.\]

If we we want to construct an actual polygon from such data we first define $\alpha_0,\ldots,\alpha_{n-1}$ as

\[\alpha_j=\kappa_1+\ldots+\kappa_j.\]

From these we define normalized edge vectors $T_j=e^{i\alpha_j}$ and finally the polygon itself: For $j=0,\ldots,n$ we set

\[\gamma_j=\ell_0 T_0+\ldots+\ell_{j-1} T_{j-1}.\]

The direction of the edge joining $\gamma_j$ to $\gamma_{j+1}$ is given by $T_j=e^{i\alpha_j}$ with . Then the position $\gamma_n$ of the last vertex (equal to $\gamma_0$ for a closed polygon) is given a

\[\gamma_n=\ell_0 e^{i\alpha_0}+\ldots +\ell_{n-1} e^{i\alpha_{n-1}}.\]

Theorem (Schläfli Formula): From given parameters

\[(\ell_0,\dots,\ell_{n-1},\kappa_1,\ldots,\kappa_{n-1})\in (0,\infty)^{n-1} \times (-\pi,\pi)^{n-2}\]

construct a polygon $\gamma_0,\ldots,\gamma_n$ as described above. Consider a variation $(\dot{\ell}_0,\dots,\dot{\ell}_{n-1},\dot{\kappa}_1,\ldots,\dot{\kappa}_{n-1})$ of these parameters and define

\[\dot{\kappa}_n:=-(\dot{\kappa}_1+\ldots+\kappa_{n-1}).\]

Then the corresponding variation of $\gamma_n$ will be given by

\[\dot{\gamma}_n=\sum_{j=0}^{n-1} \, \dot{\ell}_j T_j-i \sum_{j=1}^{n}  \dot{\kappa}_j \gamma_j.\]

Proof: For $j=0,\ldots,n$ define $\dot{\alpha}_j:=\sum_{k=1}^j \,\dot{\kappa}_k$.

Then $\dot{\alpha}_0=\dot{\alpha}_n=0$ and

\begin{align*}\dot{\gamma}_n &=\sum_{j=0}^{n-1} \, (\dot{\ell}_j +i\ell_j \dot{\alpha}_j) e^{i\alpha_j}\\\\ &= \sum_{j=0}^{n-1} \, \dot{\ell}_j T_j +i \sum_{j=1}^{n-1}  \dot{\alpha}_j (\gamma_{j+1}-\gamma_j) \\\\ &=  \sum_{j=0}^{n-1} \, \dot{\ell}_j T_j+i \dot{\alpha}_{n-1}\gamma_n -\dot{\alpha}_1 \gamma_1-i \sum_{j=2}^{n-1}  (\dot{\alpha}_j-\dot{\alpha}_{j-1}) \gamma_j\\\\ &=\sum_{j=0}^{n-1} \, \dot{\ell}_j T_j-i (\dot{\alpha}_n-\dot{\alpha}_{n-1})\gamma_n -i(\dot{\alpha}_1-\dot{\alpha_0}) \gamma_1-i \sum_{j=2}^{n-1}  \dot{\kappa}_j \gamma_j\\\\  &=\sum_{j=0}^{n-1} \, \dot{\ell}_j T_j-i \sum_{j=1}^{n}  \dot{\kappa}_j \gamma_j.\end{align*}

$\square$

Let $(\gamma_0,\ldots,\gamma_n)$ be a regular polygon in the plane $\mathbb{R}^2$. Then there are unique real numbers $\ell_0, \ldots ,\ell_{n-1}>0$ and unit vectors $T_0,\ldots,T_{n-1}\in S^1$ such that the edge vectors of $\gamma$ have the form

\[\gamma_{j+1}-\gamma_j=\ell_j T_j.\]

Furthermore, it never happens that $T_{j+1}=-T_j$ and therefore there are unique real numbers $\kappa_1,\ldots,\kappa_{n-1}$ such that

\begin{align*}-\pi &< \kappa_j < \pi \\\\ T_j &= e^{i\kappa_j}\,T_{j-1}.\end{align*}

It is easy to see that we have

\[T_j=e^{i\alpha_j}\,T_0\]

with

\[\alpha_j=\sum_{k=1}^j \,\kappa_j.\]

So $\kappa$ determines $T$ uniquely up to a multiplicative constant $a=T_0$ of norm one. Together with the edge lengths $\ell_0,\ldots, \ell_{n-1}$ the tangent directions $T$ in turn determine $\gamma$ up to an additive (translational) constant $b=\gamma_0$:

\[\gamma_j=\gamma(0)+\sum_{k=0}^{j-1}\, T_j.\]

Thus for each collection of edge length $\ell_0,\ldots, \ell_{n-1}$ and each curvature function $\kappa$ there exists a discrete curve $\gamma$ with curvature $\kappa$. Every other such curve $\tilde{\gamma}$ differs from $\gamma$ only by a euclidean motion:

\[\tilde{\gamma}=a \gamma+b\]

with $|a|=1$.

For a closed discrete curve we must have $T_n=T_0$ which means that there has to be an integer $m\in \mathbb{Z}$ such that

\[\sum_{k=1}^n\, \kappa = \alpha_n=2\pi m.\]

$m$ is called the tangent winding number of $\gamma$.

A discrete curve in $\mathbb{R}^n$ is just a finite sequence $\gamma=(\gamma_0,\ldots,\gamma_n)$ of points in $\mathbb{R}^n$. Given a partition

\[a=t_0 < t_1 <t_2 <\ldots <t_n=b\]

of a closed interval $[a,b]\subset \mathbb{R}$ we can define a piecewise linear path $\hat{\gamma}: [a,b] \to \mathbb{R}^n$ by setting for $t_{j-1}\leq t \leq t_j$

\[\hat{\gamma}(t) = \gamma_{j-1}+(t-t_{j-1}) (\gamma_j-\gamma_{j-1}).\]

We call $\hat{\gamma}$ a parametrization of $\gamma$. Any partitioning of another interval $[\tilde{a},\tilde{b}]$ into $n$ sub-intervals leads to another parametrization $\tilde{\gamma}$ of $\gamma$.

$\gamma$ is called embedded if $\hat{\gamma}$ is injective. It is called regular if $\hat{\gamma}$ is at least locally injective, i.e. for each $t\in [a,b]$ there is an $\epsilon >0$ such that $\hat\gamma |_{(t-\epsilon,t+\epsilon)}$ is injective. It is easy to see that these definitions do not depend on the choice of the parametrization $\hat{\gamma}$.

The length of a discrete curve is defined as

\[L(\gamma_0,\ldots,\gamma_n)=\sum_{j=1}^n \,|\gamma_n-\gamma_{j-1}| .\]

A parametrization $\hat{\gamma}$ of $\gamma$ is called a parametrization by arclength if each edge has the same length as the corresponding parameter interval:

\[|\gamma_n-\gamma_{j-1}|=t_j-t_{j-1}.\]

Closed discrete curves are defined in a way similar to to the smooth case: They are pairs $(\gamma,n)$ where $\gamma$ is an $n$-periodic sequence of points in $\mathbb{R}^n$. For practical purposes they are the same thing as a discrete curve $(\gamma_1,\ldots,\gamma_n)$ together with the convention that indices are to be counted modulo $n$.