Eclipse
During the whole course we will work with Eclipse. It can be downloaded from the Eclipse website and is easily installed at home. In general Eclipse is quiet well documented – see the documentation.
For the communication we will use Subversive – a subversion team provider – which can be installed from the Eclipse project update sites. See here for installation instructions.
At the university different versions of Eclipse with installed Subversion are found under /net/MathVis/. We will use Eclipse Juno. Start it with the command
/net/MathVis/eclipse_juno_java_linux64bit_with_subversive/eclipse
in the terminal. Note: the default version installed at TU is also Juno but without Subversion. Make sure you start the correct one.
SVN-Repositories
For the communication we will use subversion-server of the university. This is also the place where the repositories of jTEM and jReality lie. The server addresses are
TODO 1: Start Eclipse, open the SVN Repository Exploring perspective, and create a new Repository Location for jTEM. Check out the following projects:
- beans
- function
- java2d
- java2dx
- jrworkspace
- mfc
- modelling
- numericalMethods
The exercises shall be stored at the course-repository which lies at the following address:
http://fs.math.tu-berlin.de:8000/svn/MathVis/SS13
The username and password is sent to you by mail. You can check it e.g. via the terminal with pine.
TODO 2: Switch in Eclipse to the Java Perspective and create a new project. The project name shall be of the form “accountname_yourname”. Create a package with the name “exercise” in your project and share the project into the course-repository. You”ll find the command in the team-menu (right-click on project folder).
Java2dViewer
To visualize plane geometries we will use the Viewer2D from java2d in combination with jrworkspace, which with its plugin system is also an important ingredient of jReality. The result is the Java2dViewer, which can be found in the plugin package of java2dx.
How the Java2dViewer is used is demonstrated in the main-method of the class SubdividedPolygonPlugin. The class can be found in the discretePlaneCurves project, which lies in the course-repository and will be the basis for what we will do in the beginning of this course.
TODO 3: Check out the project discretePlaneCurves from the course-repository and run the SubdividedPolygonPlugin.
The whole system is based on plugins, which can be registered at the viewer. If the plugin extends View2DShrinkPanelPlugin a panel appears (if not specified differently) in the right slot of the viewer.
The most important method of such a plugin is the install method, which makes a communication between different plugins possible. The argument of this method, the Controller, knows all the available plugins and can be asked for them.
Typically this looks as follows:
private Viewer2D viewer= null;
private SubdividedPolygon2D polygon= null;
…
public void install(Controller c) throws Exception {
viewer = c.getPlugin(Java2DView.class).getViewer2D();
polygon = c.getPlugin(SubdividedPolygonPlugin.class)
.getSubdividedPolygon();
…
super.install(c);
}
So, e.g, the DualPolygonPlugin can get the polygon from the SubdividedPolygonPlugin and generate the corresponding dual curve. But what is a dual curve? How does it look like?
TODO 4: Create a class with name DualCurveViewer in the exercise-package of your project. Its main-method shall initialize a Java2dViewer, register the DualPolygonPlugin, and start the viewer. Hint: The SubdividedPolygonPlugin has a main-method that starts a viewer. Run the application and play around a while. If everything is correct, commit the changes to the repository.
In order to produce nice pictures the appearance of the curves can be changed and the result can be exported as pdf. The following pictures show two examples.


If one really wants to understand what is going on, we need a bit more mathematical background.
Dual Curves
If we start with a smooth 1-parameter family of lines \(L\) in the plane, then there is a smooth curve \(\gamma\) such that \(\gamma\) is tangent to each curve in the family at some point – this curve \(\gamma\) is called the envelope of \(L\). The whole story directly translates to the discrete world. If you have a sequence of lines in the plane \(L\), then there corresponds a discrete curve \(\gamma\) to it. The construction of \(\gamma\) is elementary: two successive lines have an intersection. This gives a sequence of points, i.e. a discrete curve.
But wait, where do two parallel lines intersect? Right, they do not intersect in \(\mathbb{R}^2\), but in an infinitely far “ideal” point. If want to make this precise, we have to speak about the real projective plane. Here every pair of distinct lines intersects in exactly one point. We will give a short impression. For a serious treatment see the literature. There are lots of books on this subject. I recommend the lecture notes of Nigel Hitchin on projective geometry and quadrics, which are free available on his homepage http://people.maths.ox.ac.uk/hitchin/.
Real Projective Space. The \(n\)-dimensional real projective space consists of all (unoriented) lines through the origin of a \(n+1\)-dimensional real vector space \(V\). To make this more rigorous, introduce an equivalence relation \(\sim\) on \( V_0:= V\setminus\{0\}\) as follows\[ x\sim y:\Leftrightarrow x= \lambda y ,\quad 0\not=\lambda\in\mathbb{R}.\]
We denote the equivalence class of a vector \(x\) by \([x]\). The \(n\)-dimensional real projective space \(P(V)\) is then the quotient space with respect to the defined equivalence relation:\[ P(V)= V_0/_\sim.\]
If \(V\) is 2-dimensional we call \(P(V)\) a projective line. If \(V\) is 3-dimensional we call it a projective plane.
Curves in the Projective Plane. For now we are only interested in the projective plane \(\mathbb{RP}^2= P(\mathbb{R}^3)\). Each plane \(U\subset\mathbb{R}^3\) in \(\mathbb{R}^3\) can be identified with \(\mathbb{R}^2\). If \(U\) does not contain the origin, each point in \(U\) can be identified with a point in \(\mathbb{RP}^2\) by \(x \mapsto [x]\). The points in \(\mathbb{RP}^2\) which are not obtained this way are exactly the vectors that are parallel to \(U\). This is a 2-dimensional subspace of \(\mathbb{R}^3\) – the projectivization of which is a real projective line. Hence, we can consider the real projective plane as the union of \(\mathbb{R}^2\) with a real projective line \(\mathbb{RP}^1\) – the “ideal line”:\[ \mathbb{RP}^2= \mathbb{R}^2\cup \mathbb{RP}^1.\]
In this sense each plane curve \(\gamma=(\gamma_1,\gamma_2)\) lifts to a projective one. If we choose \(U= \{x\in\mathbb{R}^3\mid x_3=1\}\) then the map is simply given by \[ \gamma \mapsto \Gamma = [\gamma_1,\gamma_2,1]. \]
Opposite, if we have a projective curve \(\Gamma=[\Gamma_1,\Gamma_2,\Gamma_3]\) that does not pass the ideal line, i.e. \(\Gamma_3\not= 0\), then we can get corresponding curve in \(\mathbb{R}^2\) by normalizing the last component to \(1\):\[ \Gamma \mapsto \gamma= (\Gamma_1/\Gamma_3,\Gamma_2/\Gamma_3).\]
If \(\Gamma\) is a general projective curve, we call the part which does not intersect the ideal line the finite part of \(\Gamma\).
Curves of lines. What does this have to do with families of lines in \(\mathbb{R}^2\)? A line \(L\) in the real plane can given by an equation\[ L_{(a,b,c)}=\{(x,y)\in \mathbb{R}^2 \mid ax+by-c=0\}\quad a,b,c\in \mathbb{R}.\]
So we see that lines are essentially given by vectors in \(\mathbb{R}^3\). But the equation can be multiplied by an arbitrary non-zero scalar while the line does not change. Thus the line corresponds to a point in the projective plane.
How the line can be recovered from that point \([a,b,-c]\in\mathbb{RP}^2\)? Consider the linear form \[ \eta_{(a,b,c)} (x,y,z) = ax+by-cz. \]
The projectivization of its kernel is a projective line the finite part of which is exactly \(L_{(a,b,c)}\).
So we have seen that plane curves and smooth families of lines both can be regarded as curves in the projective plane.
Polarity. Let \(Q\) be an indefinite non-degenerate quadratic form on \(\mathbb{R}^3\). By Sylvester’s law of inertia every such form on \(\mathbb{R}^3\) arises from a standard form by a change of basis. We can assume without loss of generality that the form is represented by the matrix the following matrix: \[Q=\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&-1 \end{pmatrix}.\]
The quadric \(\mathbf Q \subset \mathbb{RP}^n\) is defined as the zero set of \(Q\), i.e.\[ \mathbf Q= \{[x]\in \mathbb{RP}^2 \mid Q(x,x)=0\}.\]
Note, that the zero set is also well defined in the projective setting. The intersection with the plane \(\{z=1\}\) is just a round circle. If one instead intersects it with other planes one gets the usual plane conic sections as shown in the picture below.

With \(Q\) we get an isomorphism from \(\mathbb{R}^3\) to \(\mathbb{R}^3\). It is given by the following map\[ (a,b,c)\mapsto (a,b,-c).\]
Under this map the point \((a,b,c)\) is identified with \(L_{(a,b,c)}\), called the polar of the point. The correspondence has also a nice geometric construction as shown in the next picture (taken from here).

Using this duality we get for each projective curve \(\gamma\) a dual projective curve \(\Gamma\).
The dual curve \(\Gamma\) of a curve \(\gamma\) in \(\mathbb{R}^2\) is defined as the envelope of the line field corresponding to the dual curve of the projective curve induced by \(\gamma\). Hopefully, this won’t lead to confusion.
The curve does not have to stay in the finite part, but can also pass the ideal line as shown in the picture below.

The evolute of a curve
Smooth case. Let \(\gamma\) be a plane curve. The evolute of \(\gamma\) is defined as the envelope of the normal field of \(\gamma\). It can be shown that the evolute \(\hat\gamma\) is given by \[ \hat\gamma= \gamma+\tfrac{1}{\kappa}N,\] where \(N\) denotes the normal field and \(\kappa\) the curvature of \(\gamma\). If \(\gamma\) was arclength parametrized \(\kappa\) is given by\[ T^\prime= \kappa N. \]
The osculating circle of \(\gamma\) is the circle that touches \(\gamma\) of second order. Its center \(c_\kappa\) is called the center of curvature. Its radius \(R\) and \(\kappa\) are related by\[ R= \left|\tfrac{1}{\kappa}\right|. \] In other words: The evolute is the trace of the center of curvature.

Discrete case. While it is clear what the normal field is in the smooth case, there are different possible choices of normal directions in the discrete case. It is even not clear whether they sit at vertices or on the edges, but there are good possible choices.
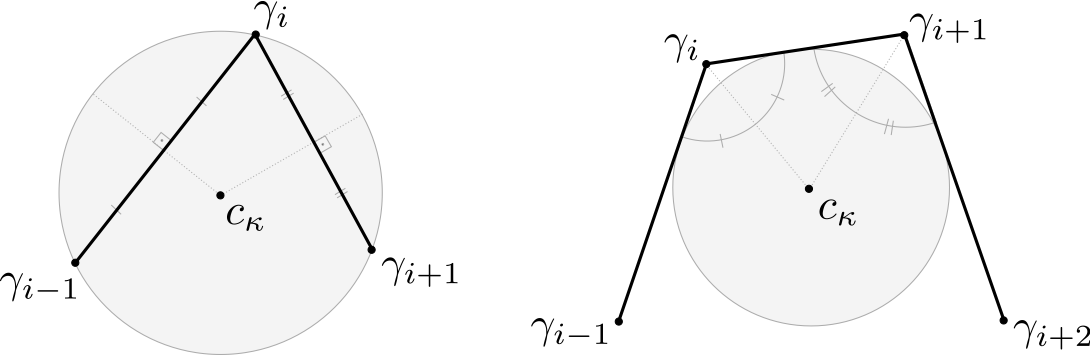
Possibility 1: Define the normal spaces at edges. Here the most obvious choice is to take the edge bisector (see here e.g.). The edge bisectors of two successive edges meat in the circumcenter of the triangle that is determined by the two involved edges.
Hence one possibility of a discrete evolute is to define it as the sequence of circumcenters of three successive vertices.
In fact, we can easily translate that into the projective curve setting, i.e. we can specify the normal field by a projective curve. Drawing the envelope yields nice results. Below you find two examples of evolutes defined using edge bisectors.


Possibility 2: Define the normal spaces at vertices. Here the angle bisectors that cross the discrete curve seem to be a good choice. The angle bisectors of two successive vertices meat in the center of a circle that touches the three edges that incident with the vertices – another osculating circle.
Homework: Implement both definitions of a discrete evolute, i.e. write a plugin that can switch between the two definitions. Use for it the DualPolygon2D class, which allows you to specify a projective curve, which interprets a dual projective curve as a curve of lines in the plane. The envelope is drawn automatically.