Let $\gamma_1,\ldots,\gamma_n$ be a regular polygon in $\mathbb{R}^2=\mathbb{C}$. A second polygon $\tilde{\gamma}_1,\ldots,\tilde{\gamma}_n$ is said to be a Darboux transform of $\gamma$ if three conditions are satisfied. The first two conditions are:
1) The distance between corresponding points is a fixed number $\ell$. This means for all $j$ we have
\[|\tilde{\gamma}_j-\gamma_j|=\ell.\]
2) Corresponding edges have the same length. This means
\[|\tilde{\gamma}_{j+1}-\tilde{\gamma}_j|=|\gamma_{j+1}-\gamma_j|.\]
These two conditions are trivially met by a polygon $\tilde{\gamma}$ that is just a translate of $\gamma$, i.e. $\tilde{\gamma}_j=\gamma_j+a$ for some fixed $a\in \mathbb{R}^2$. In this case for all $j$ the four points $\gamma_j, \gamma_{j+1}, \tilde{\gamma}_j,\tilde{\gamma}_{j+1}$ form a parallelogram. To eliminate this trivial solution we add a third condition:
3) Given the points $\gamma_j,\gamma_{j+1}$ and $\tilde{\gamma}_j$ the next point $\tilde{\gamma}_{j+1}$ is chosen to be different from $\tilde{\gamma}_j+(\gamma_{j+1}-\gamma_j)$, if possible.
Here the word “if possible” refer to the case where $\gamma_j,\gamma_{j+1},\tilde{\gamma}_j$ lie on a straight line. In this case the parallelogram solution is the only one that complies with the first two conditions.
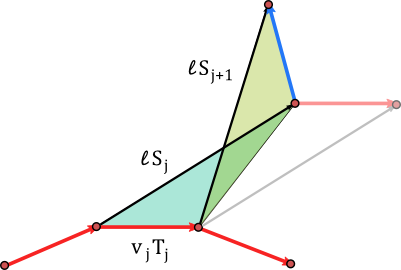
We denote the edge lengths by
\[v_j=|\gamma_{j+1}-\gamma_j|\]
and introduce unit vectors $T_j$ and $S_j$ such that
\begin{align*}\gamma_{j+1}-\gamma_j&=v_j T_j \\\\ \tilde{\gamma}_j -\gamma_j &= \ell S_j.\end{align*}
Now it is easy to see that the three conditions above amount to saying that $S_{j+1}$ is obtained from $S_j$ (the parallelogram solution) by reflecting it in that diagonal of the parallelogramm that does not contain $\gamma_j$.
The direction of this diagonal is given by the vector $\ell S_j – v_j T_j$. Reflection in a vector $a\in \mathbb{C}$ is the map
\[z\mapsto \frac{a}{\bar{a}}\bar{z}.\]
Using this we obtain
\[S_{j+1}=\frac{\ell S_j – v_j T_j}{\ell \bar{S}_j – v_j \bar{T}_j}\bar{S}_j=\frac{\ell S_j -v_j T_j}{\ell -v_j \bar{T}_j S_j}.\]
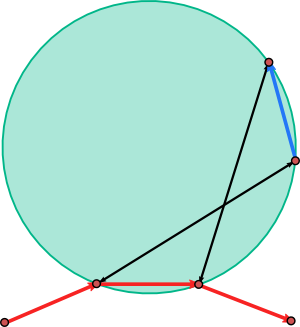
Obviously the four points $\gamma_j, \gamma_{j+1}, \tilde{\gamma}_j,\tilde{\gamma}_{j+1}$ lie on a circle. One might formulate this by saying that the polygons $\gamma$ and $\tilde{\gamma}$ are “enveloped” by a sequence of circles in such a way that the arclength on the two envelopes is in correspondence.