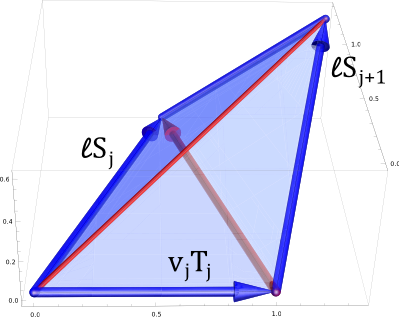
Let $\gamma_1,\ldots,\gamma_n\in \mathbb{R}^3$ be a regular discrete space curve. We are looking for another discrete space curve $\tilde{\gamma}$ that satisfies the first two conditions we had in the planar case: The distance between corresponding points $|\tilde{\gamma}_j-\gamma_j|$ is a constant $\ell$ and corresponding edges of $\gamma$ and $\tilde{\gamma}$ have the same length. Then (with a notation as in the previous post) we see that compared two the planar case we have a whole one-parameter family of possible choices for $S_{j+1}$: The vector $S_{j+1}$ can be the result of rotating $S_j$ around $\ell S_j + v_j T_j$ by any chosen angle.
One can imagine to start with a parallelogram with sides $v_j T_j$ and $\ell S_j$. The parallelogram is then folded around the diagonal whose direction is $\ell S_j-v_jT_j$.
Folding by 180 degrees corresponds to the Darboux-transformations we studied in the two-dimensional setting. It is given by the map
\[y\mapsto (\ell S_j-v_jT_j)y(\ell S_j-v_jT_j)^{-1}.\]
Any other folding angle (except for angle zero that would leave us with the parallelogram) can be realized as
\[y \mapsto qyq^{-1}\]
with $q$ of the form
\[q=r+\ell S_j-v_jT_j.\]
Here $r$ is an arbitrary real number. This leads to
\[S_{j+1}=(r+\ell S_j-v_jT_j)S_j(r+\ell S_j-v_jT_j)^{-1}\].
Definition: A discrete space curve $\tilde{\gamma}$ is called a Darboux transform of $\gamma$ with rod length $\ell$ and twist $r$ if
\[\gamma_j=\gamma_j+\ell S_j\]
and $S_1,\ldots, S_n$ satisfy the above equation.
Let us omit the subscript $j$ and use a subscript “+” instead of $j+1$. Combining then in the above formula the $S$ in the middle with the left bracket we see that the map $S\mapsto S_+$ is fractional linear:
\[S_+=((r -v T) S-\ell)((r -vT)+\ell S)^{-1}.\]
To investigate this map further we write $S$ as the stereographic projection with center $-T$ of some point $Z\in \mathbb{R}^3$ orthogonal to $T$:
\begin{align*} S &=(1-ZT)T(1-ZT)^{-1} \\\\ &=(T+Z)(1-ZT)^{-1} \\\\ &= T(1-ZT)(1+ZT)^{-1}.\end{align*}
The first line shows that $S\in S^2$ for $Z\perp T$. The second line shows that $Z\mapsto S$ is fractional linear. The last line shows that $S=Z$ in case $|Z|=1$. Let us plug this into the last formula for $S_+$:
\begin{align*}S_+&= ((r-vT)(T+Z)-\ell (1-ZT)((r-vT)(1-ZT)+\ell(T+Z))^{-1} \\\\ &=(((v-\ell)+rT)+(r-(v+\ell)T)Z)((r+(\ell-v)T)+((\ell+v)+rT)Z)^{-1} \\\\ &= \left(T+Z\frac{(\ell+v)-rT}{(\ell-v)-rT}\right)\left(1+TZ\frac{(\ell+v)-rT}{(\ell-v)-rT}\right)^{-1}.\end{align*}
Here the fractional notation is justified because the quaternions involved all commute. Thus in terms of the sterographic coordinate $Z$ the transition from $S$ to $S_+$ is just multiplication
\[Z+=MZ=Z\overline{M}\]
by a quaternion
\[M = \frac{(\ell+v)+rT}{(\ell-v)+rT}.\]
In the case $r=0$ this is in perfect accordance with the results of an earlier post.