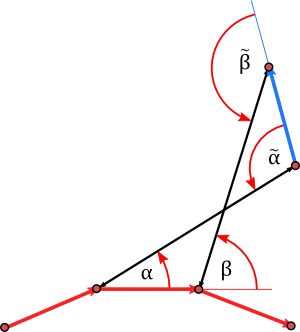
As in the last post let $\gamma$ be a discrete curve in the $\mathbb{C}$ and $\tilde{\gamma}= \gamma+ \ell S$ be a Darboux transformation. Denote by $\alpha_j$ and $\beta_j$ the angles from the edges $T_J$ of $\gamma$ to the rod directions $S_j$ and $S_{j+1} respectively. Then
\begin{align*}S_j &= e^{i \alpha_j} T_j \\\\ S_{j+1}&= e^{i \beta_j} T_j.\end{align*}
We know that $S$ satisfies
\[ S_{j+1}=\frac{\ell S_j- v_j T_j}{\ell-v_j \bar{T}_j S_j}.\]
This yields
\[ e^{i\beta_j}=\frac{\ell e^{i\alpha_j}- v_j}{\ell-v_j e^{i\alpha_j}}.\]
Using the formula
\[e^{i\alpha}=\frac{1+it}{1-it}\]
where
\[t:=\tan \frac{\alpha}{2}\]
we then have
\begin{align*} e^{i\beta_j}&=\left(\ell \frac{1+it_j}{1-it_j}- v_j \right) \left(\ell-v_j \frac{1+it_j}{1-it_j} \right)^{-1} \\\\ &=\left(\frac{(\ell -v_j)+(\ell +v_j)it_j}{1-it_j}\right) \left( \frac{(\ell-v_j )-(\ell+v_j )it_j}{1-it_j} \right)^{-1} \\\\ &= \frac{1+i \mu_j t_j}{1-i \mu_j t_j} \,.\end{align*}
where
\[ \mu_j= \frac{\ell+v_j}{\ell-v_j}.\]
From this we conclude
\[\tan \frac{\beta_j}{2}=\mu_j \tan \frac{\alpha_j}{2}.\]
With the notation
\begin{align*}t_j&:=\tan \frac{\alpha_j}{2}\\\\ \tau_j&:=\tan \frac{\kappa_j}{2}\end{align*}
we obtain
\begin{align*}\tau_j&=\tan \frac{\beta_{j-1}-\alpha_j}{2}\\\\ &= \frac{\mu_{j-1} t_{j-1}-t_j}{1+\mu_{j-1} t_{j-1} t_j}.\end{align*}
The corresponding quantities for the Darboux transform $\tilde{\gamma}$ are
\begin{align*}\tilde{\alpha}_j &=\pi-\beta_j \\\\ \tilde{\beta}_j &= \pi- \alpha_j \\\\ \tilde{\tau}_j&=\tan \frac{\beta_j-\alpha_{j-1}}{2}\\\\ &= \frac{\mu_j t_j-t_{j-1}}{1+\mu_j t_j t_{j-1}}.\end{align*}
Note that we arrive at $\tilde{\tau}_j$ starting from $\tau_j$ if we interchange the roles of $t_{j-1}$ and $t_j$ and replace $\mu_{j-1}$ by $\mu_j$. If we apply this rule to
\begin{align*}1+\tau_j^2 &= \frac{(1+2\mu_{j-1} t_{j-1} t_j +\mu_{j-1}^2 t_{j-1}^2 t_j^2) + (t_j^2 -2 \mu_{j-1} t_{j-1} t_j +\mu_{j-1}^2 t_{j-1}^2)}{(1+\mu_{j-1} t_{j-1} t_j)^2} \\\\ &= \frac{(1+t_j^2)(1+\mu_{j-1}^2 t_{j-1}^2)}{(1+\mu_{j-1} t_{j-1} t_j)^2} \end{align*}
we obtain
\[1+\tilde{\tau}_j^2=\frac{(1+t_{j-1}^2)(1+\mu_j^2 t_j^2)}{(1+\mu_j t_j t_{j-1})^2}\]
Now the following is easy to prove:
Theorem: If $\gamma$ is a closed polygon in $\mathbb{R}^2$ with equal edge lengths and $\tilde{\gamma}$ is a closed Darboux transform of $\gamma$ then
\[\prod_{j=1}^n (1+\tau^2) = \prod_{j=1}^n (1+\tilde{\tau}^2).\]
We can interpret this as follows: The bending energy
\[\sum_{j=1}^n \log (1+\tau_j^2)=-\sum_{j=1}^n \log (1+\cos \kappa_j)\]
is the same for $\gamma$ and $\tilde{\gamma}$.