Stereographic projection

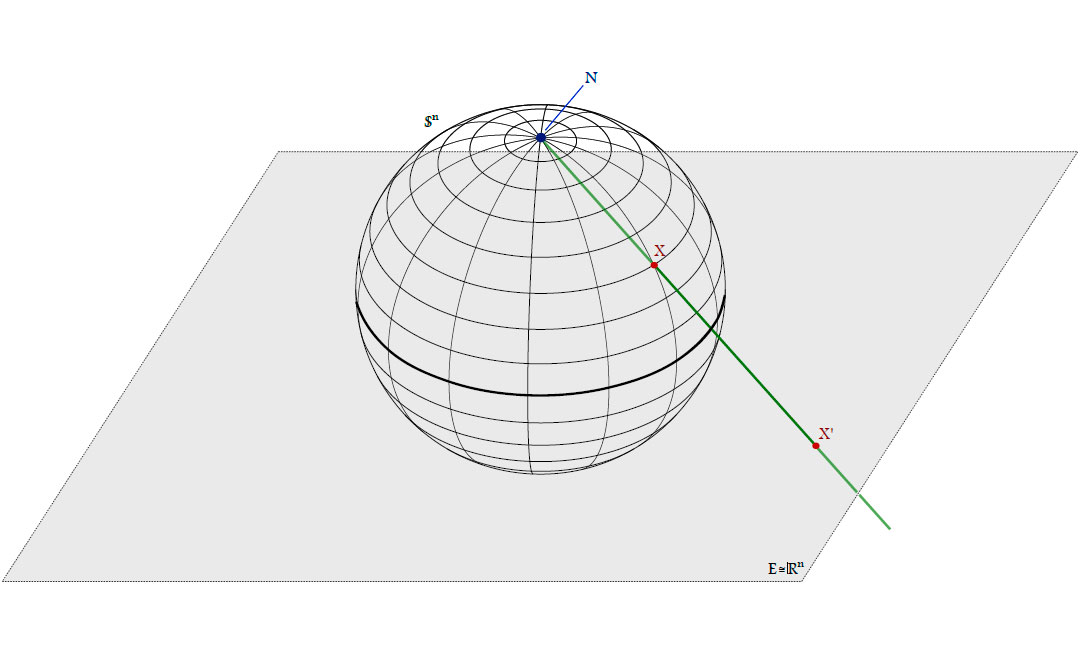
Definition. Denote the unit sphere in $\mathbb{R}^{n+1}$ by $\mathbb{S}^{n}=\left\{{x \in \mathbb{R}^{n+1}|(x,x)=1}\right\}$ and its north pole by $\mathbf{N}=e_{n+1}$.
The stereographic projection is a map $\sigma\colon \mathbb{S}^{n}\to\mathbb{R}^{n} \cup \left\{{\infty}\right\}$ from $\mathbf{N}$ to the plane
$E=\left\{{x \in \mathbb{R}^{n+1}|x_{n+1}=0}\right\} \cong \mathbb{R}^{n}$ through the equator:
\[
\sigma(X)=
\left\{
\begin{array}{ll}
\infty & \textrm{, } X = \mathbf{N}\\
l_{NX}\cap E & \textrm{, } X \neq \mathbf{N}\\
\end{array}
\right.
\]
Analytically $\sigma$ is given by
\[
\sigma(X)= \sigma\ \left(\begin{pmatrix}
x_1\\\vdots\\x_{n+1}
\end{pmatrix} \right)
= \frac{1}{1-x_{n+1}}\begin{pmatrix}
x_1\\\vdots\\x_{n+1}
\end{pmatrix}
\]
since
\[N+\lambda(X-N)=e_{n+1}+\lambda \begin{pmatrix}
x_1\\\vdots\\x_{n+1}
\end{pmatrix}
= \begin{pmatrix}
y_1\\\vdots\\y_{n}\\0
\end{pmatrix}
\Rightarrow \lambda=-\frac{1}{x_{n+1}-1}=\frac{1}{1-x_{n+1}}, X\neq N.
\]

Sphere inversion
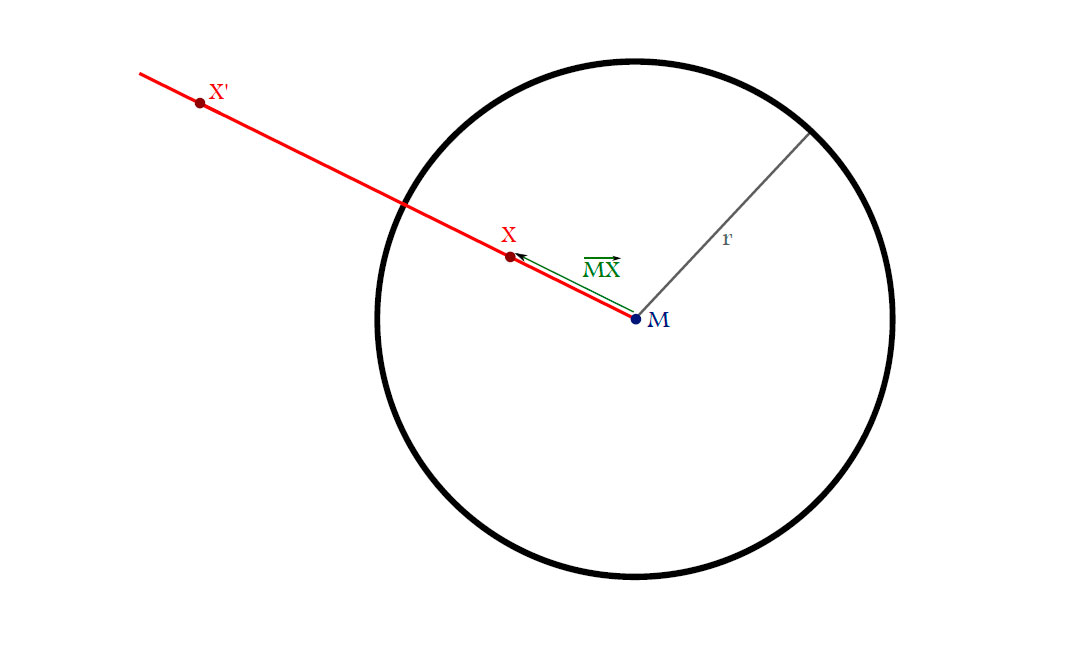
Definition. The sphere inversion $i_{M,r}\colon \mathbb{R}^{n} \cup \left\{{\infty}\right\} \to \mathbb{R}^{n} \cup \left\{{\infty}\right\}$ in the sphere
$\mathbf{S}_{M,r}=\left\{{x \in \mathbb{R}^{n}|\left\|x-M\right\|=r}\right\}$ is given by the following conditions:

• $X’$ lies on the ray $\overrightarrow{MX}$,
• $\left\|M-X\right\|\left\|M-X’\right\|=r^2$,
• $M\longleftrightarrow\infty$.

Properties of sphere inversions

1. $i_{M,r}$ is an involution,
2. $\mathbf{S}_{M,r}$ is fixed,
3. affine subspaces containing M are mapped onto themselves.

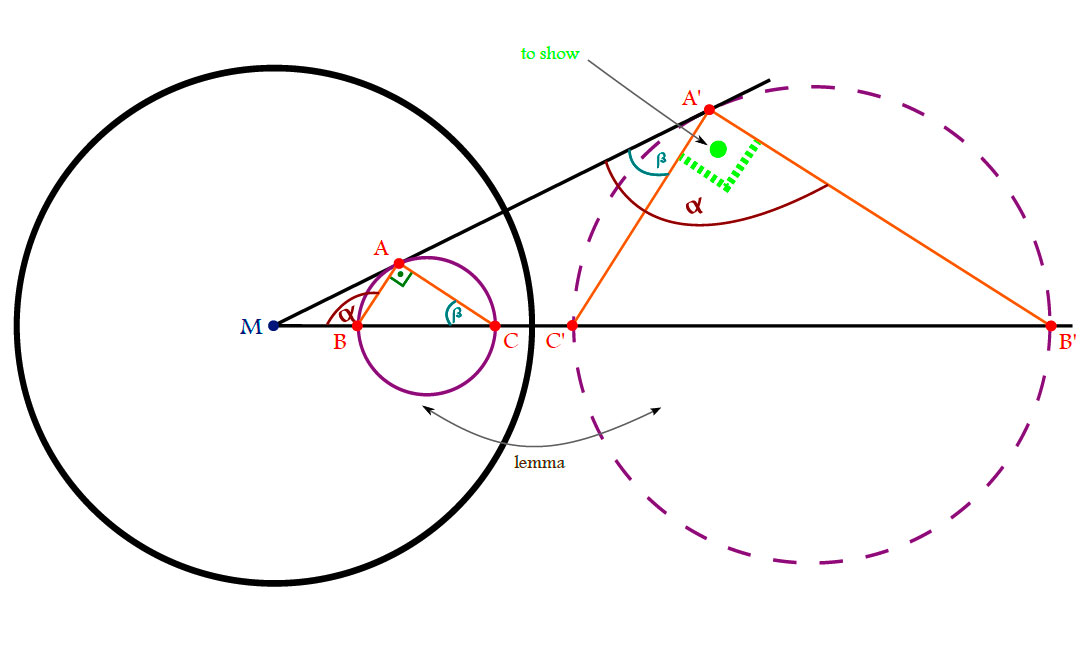
Lemma.

Proof.
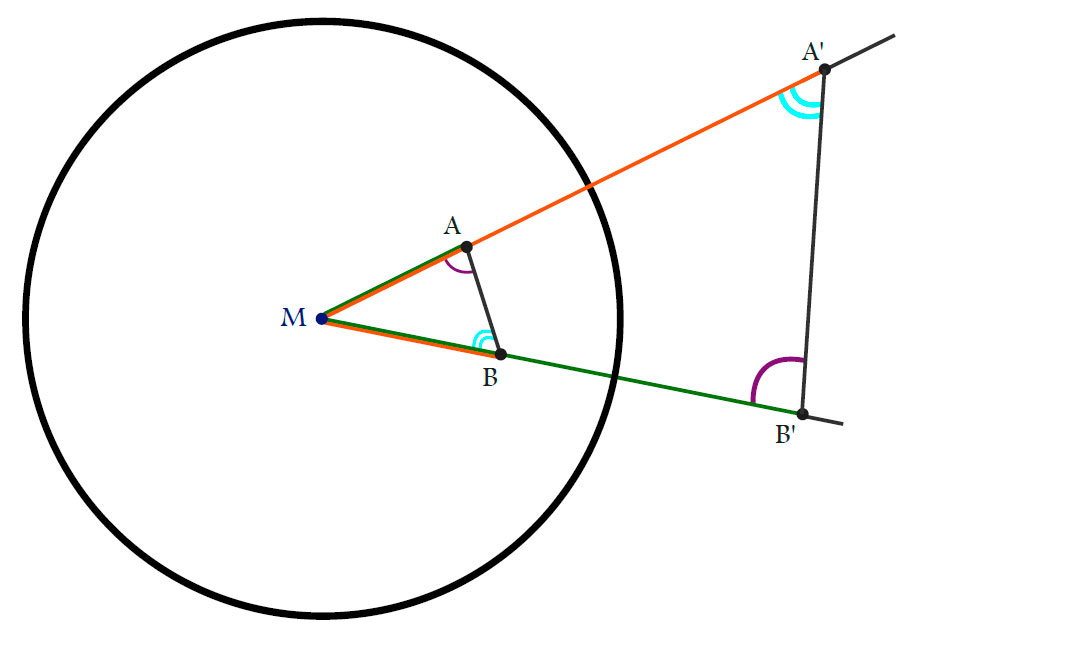
Since
\[
\left\|M-A\right\|\left\|M-A’\right\|=r^2 = \left\|M-B\right\|\left\|M-B’\right\| \iff
\frac{\left\|M-A\right\|}{\left\|M-B\right\|}=\frac{\left\|M-B’\right\|}{\left\|M-A’\right\|}
\]
we get that $\Delta AMB$ and $\Delta B’MA’$ are similar. In particular:
\[
\measuredangle MA’B’=\measuredangle ABM.
\measuredangle MAB=\measuredangle A’B’M.
\]

$\Box$

Corollary. Circles through M are mapped to lines. In particular, the line is parallel to the tangent to the circle at M.

Remark. All lines are thought to contain the point $\infty$ and are considered as circles of infinte radius.

Corollary. The stereographic projection is the restriction of the sphere inversion $i_{M,r}$ with $M=e_{n+1}$ and $r=\sqrt{2}$.

Proof.

1. The equator of $\mathbb{S}^{n}$ is fixed.
2. $\mathbb{S}^{n}$ is mapped to a plane (Corollary) through the equator (1).
3. Both inversion and stereographic projection preserve the rays.
4. The intersection points of a ray with $\mathbb{S}^{n}$ and $\mathbb{R}^{n}$ are unique, hence $i_{M,r}\Big|_{\mathbb{S}^{n}}=\sigma$.
5. $N=M\longrightarrow\infty$ by $i_{M,r}$.

$\Box$

Theorem. An inversion in a sphere:

1. maps spheres/hyperplanes to spheres/hyperplanes,
2. is a conformal map, i.e. it preserves angles.

Proof.
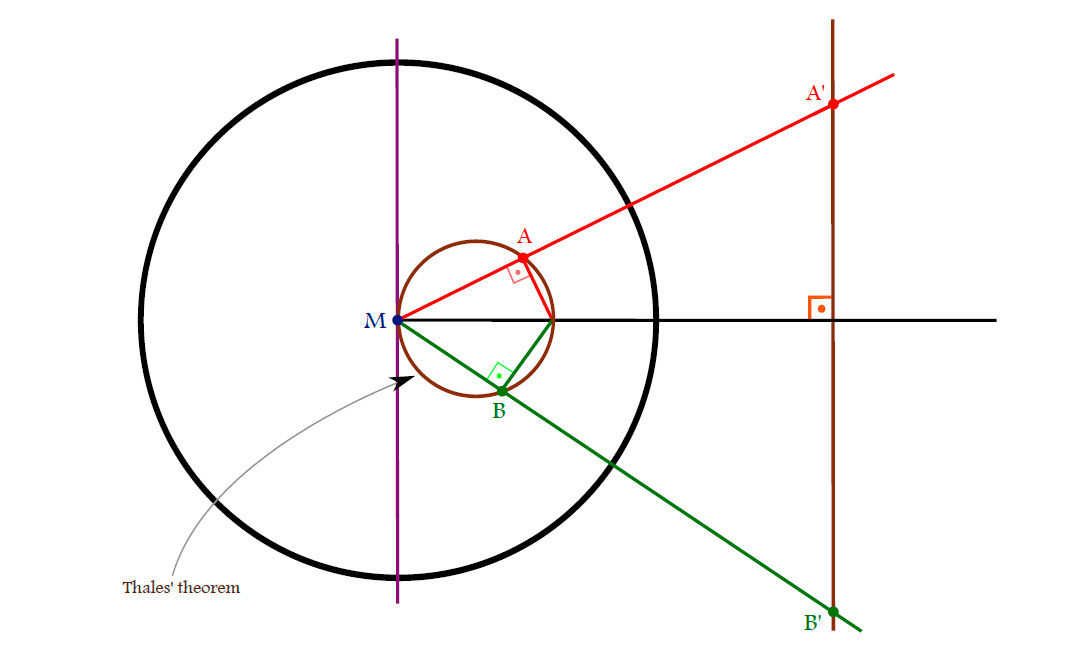
(i) Consider the following sketch:

Hence the angles $\alpha$ and $\beta$ satisfy
\[
(\pi-\alpha)+\beta+\frac{\pi}{2}=\pi \Rightarrow \alpha-\beta=\frac{\pi}{2}.
\]
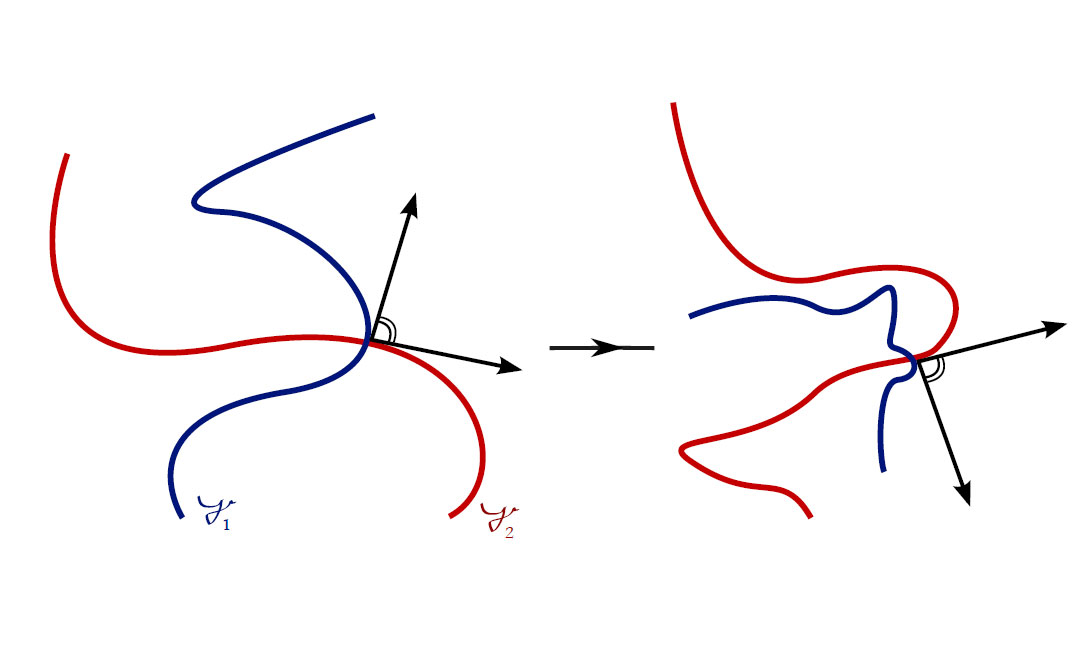
(ii) Conformality follows from the following picture

$\Box$

Remark. In general, the center of a sphere is not mapped to the center of its image by an inversion.

Corollary.

1. The stereographic projection maps spheres through the north pole to hyperplanes and spheres not through the north pole to spheres.
2. All spheres/hyperplanes are images of spheres on $\mathbb{S}^{n}$ under $\sigma$ (because $i_{0,1}$ is an involution).
3. $\sigma$ is conformal.

Formula for the sphere inversion.
Consider the second figure showing the general idea of a sphere inversion. Since $X’$ lies on the ray $XM$ we have $X’=M+\lambda(X-M), \lambda > 0$ and from the second requirement for the sphere inversion we obtain

\begin{align*}
&&\underbrace{\left\|X’-M\right\|}_{X’-M=\lambda(X-M)} \left\|X-M\right\|&=r^2\\
\Rightarrow&& \lambda \left\|X-M\right\| \left\|X-M\right\|&=r^2\\
\Rightarrow&& \lambda = \frac{r^2}{\left\|X-M\right\|^2}.
\end{align*}
Hence the sphere inversion is given by

\[
i_{M,r}=M+\frac{r^2}{\left\|X-M\right\|^2}(X-M).
\]

Theorem. The shortest piecewise continously differentiable curve in $H^n$ connecting two points $p$ and $q$ is the hyperbolic line segment between them. It’s length is $$d(p,q) = arcosh(-\langle p,q\rangle).$$

Continue reading →