Lengths/distances in $H_+^2$.

Two points $P_1$ and $P_2$ in the upper half-plane model either have the same $x$ coordinate or not. If they share the $x$ coordinate the geodesic through two points is a straight line. Otherwise it is a semi-circle. Let us calculate the hyperbolic distance between two points depending on the two cases.

Case 1.

\[
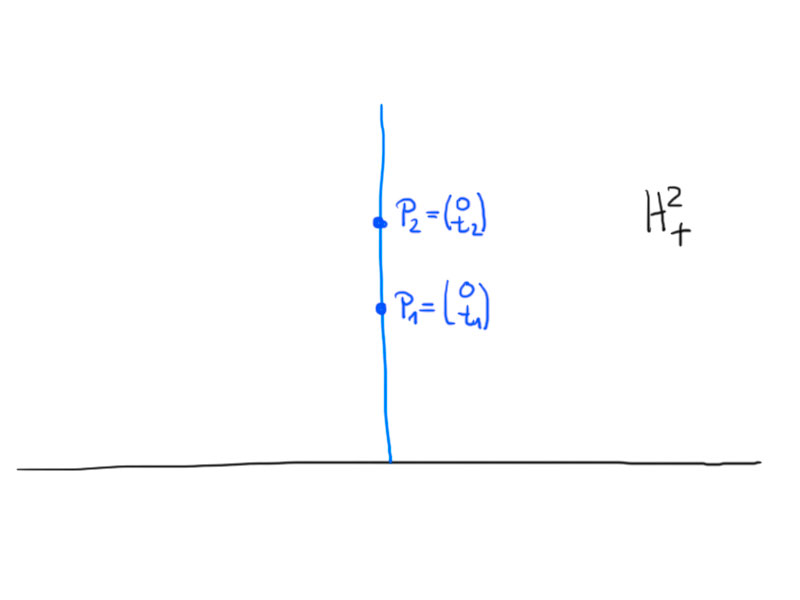
\gamma\colon[t_1,t_2]\to H_+^2\,,\ \gamma(t)=\begin{pmatrix}0\\t\end{pmatrix}\,.
\]
\begin{align*}
d(p_1,p_2)&=\int_{t_1}^{t_2}\sqrt{g_{\gamma(t)}\left(\begin{pmatrix}0\\1\end{pmatrix},\begin{pmatrix}0\\1\end{pmatrix}\right)}\mathrm dt \\
&=\int_{t_1}^{t_2}\frac1t\sqrt{\left(\begin{pmatrix}0\\1\end{pmatrix},\begin{pmatrix}0\\1\end{pmatrix}\right)}\mathrm dt=\log\frac{t_2}{t_1}\,.
\end{align*}
So the length/distance only depends on the ratio $\frac{t_2}{t_1}$, not on the values.

Case 2.

\begin{align*}
P_1&=r\begin{pmatrix}\cos\alpha_1\\\sin\alpha_1\end{pmatrix}&
P_2&=r\begin{pmatrix}\cos\alpha_2\\\sin\alpha_2\end{pmatrix}\,.
\end{align*}
Here,
\[\gamma\colon[\alpha_1,\alpha_2]\to H_+^2\,,\ \gamma(\alpha)=r\begin{pmatrix}\cos\alpha\\\sin\alpha\end{pmatrix}\,.\]
By this we get
\[d(p_1,p_2)=\int_{\alpha_2}^{\alpha_1}\frac1{\sin t}\mathrm dt=\left.\log\tan\frac t2\right\vert_{\alpha_1}^{\alpha_1}=\log\frac{\tan\frac{\alpha_1}2}{\tan\frac{\alpha_2}2}\,,\]
i.e. the distance depends on the angle, not on the radius.

Remrk.
The following maps are isometries of $H_+^2$:

• Horizontal translations, $\begin{pmatrix} x\\y\end{pmatrix}\mapsto\begin{pmatrix} x+c\\y\end{pmatrix}$,
• scalings, $\begin{pmatrix} x\\y\end{pmatrix}\mapsto\lambda\begin{pmatrix} x\\y\end{pmatrix}$ for $\lambda>0$.

Both transformations leave the Riemmanian metric invariant.

Proposition.
The distance in the Poincaré halfplane model $H_+^2\subset\C$ between two points $z_1$, $z_2$ is given by
\[\cosh d(z_1,z_2)-1=\frac{\lvert z_1-z_2\rvert^2}{2\operatorname{Im} z_1\operatorname{Im} z_2}\,.\]

Proof. Calculation using some trigonometric identities.

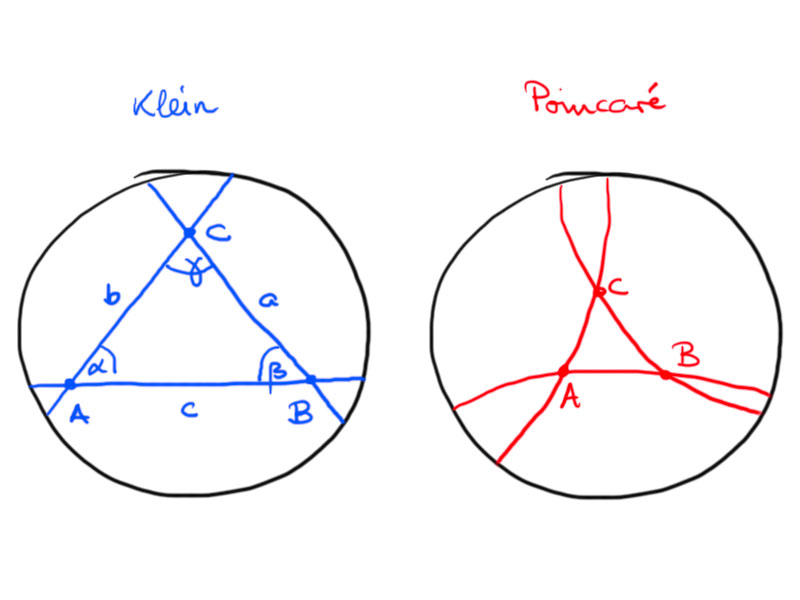
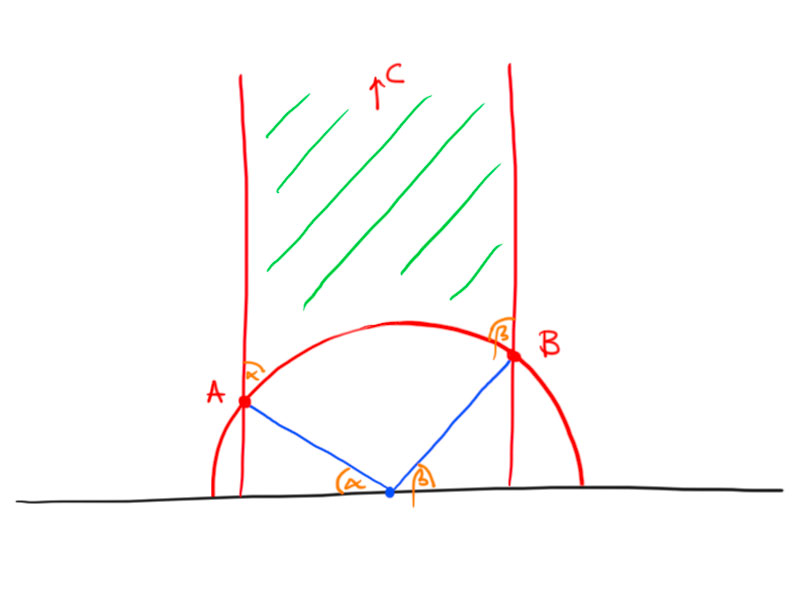
Hyperbolic triangles

Let $A$, $B$, $C$ be three points in the hyperbolic plane $H^2$ not all on one line.
Then the hyperbolic triangle is given by
\[\triangle ABC=\{\lambda A+\mu B+\nu C:\lambda,\mu,\nu>0\}\cap H^2\,.\]

The triangle defined by $A$, $B$, $C$ in the Klein model is
\[\triangle ABC=\{\lambda A+\mu B+\nu C:\lambda,\mu,\nu\geq0,\lambda+\mu+\nu=1\}\,.\]
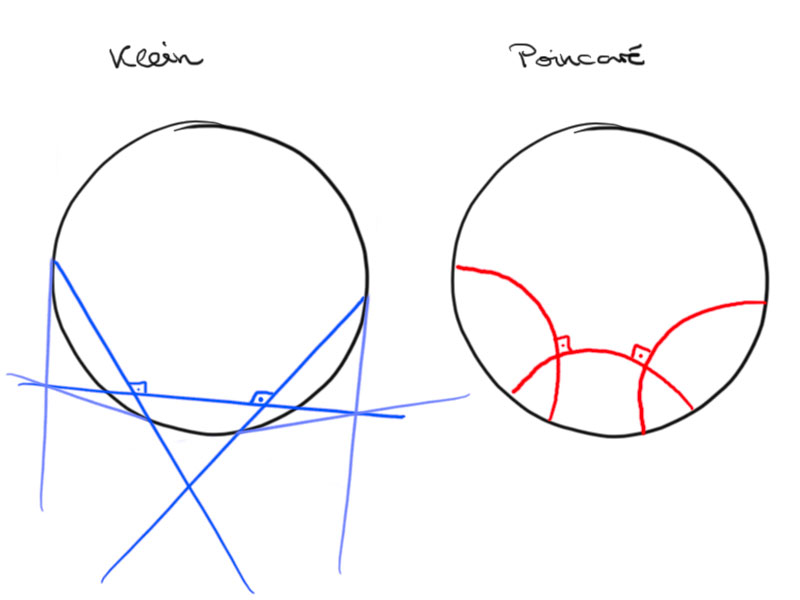
We label the vertices, angles and sides of a triangle as shown in the above picture.

Observation: $\alpha+\beta+\gamma<\pi$ for any hyperbolic triangle.
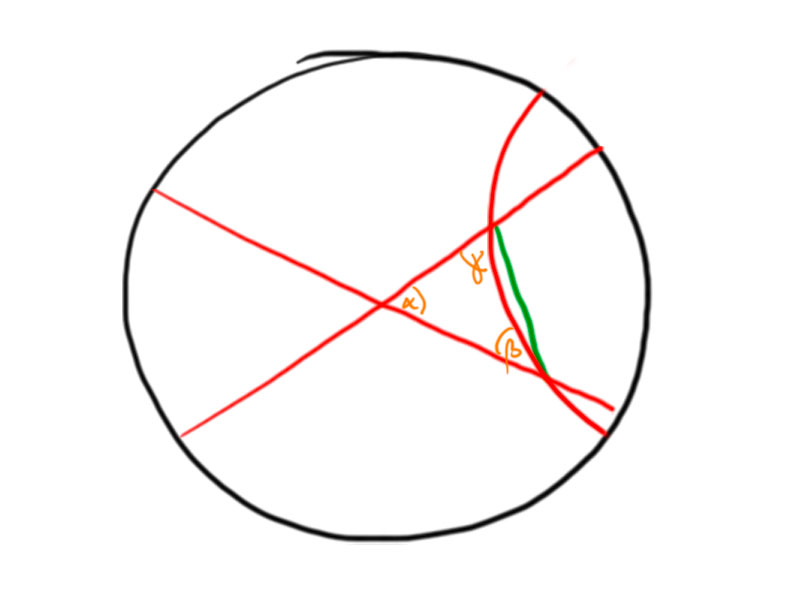
Consider a triangle in the Poincaré disc. We may use a hyperbolic motion to move $A$ to the center of the disc.

The angles between the hyperbolic lines at $B$ and $C$ are smaller than the angles of the Euclidean triangle, hence $\alpha+\beta+\gamma<\pi$.

Proposition.
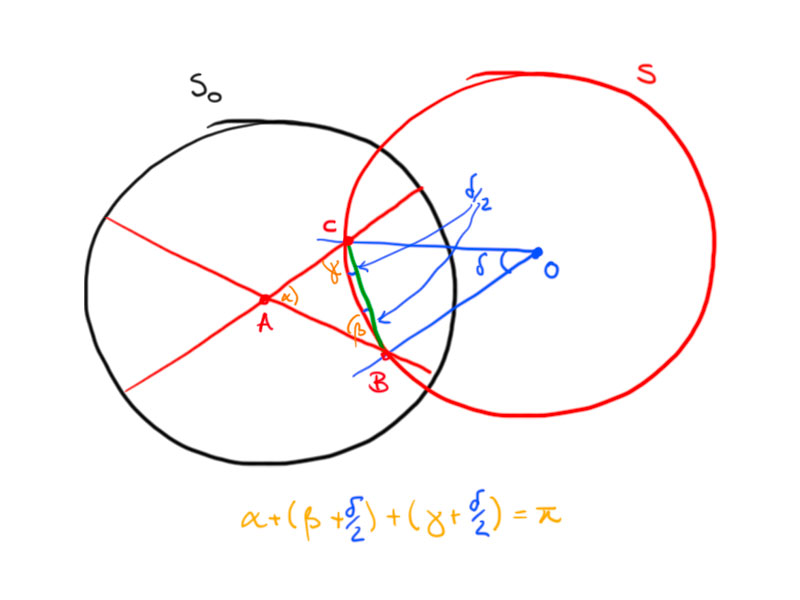
For $\alpha,\beta,\gamma>0$ with $\alpha+\beta+\gamma < \pi$ there exists a hyperbolic triangle. The triangle is unique up to hyperbolic motions.

Proof. We proof the proposition by construction: Let $\delta > 0$ such that $\alpha+\beta+\gamma+\delta = \pi$. Construct a Euclidean triangle with angles $\alpha$, $\tilde\beta = \beta+\delta/2$ and $\tilde\gamma=\gamma+\delta/2$. Then construct a circle $S$ through $B$ and $C$ such that $\angle OBC=\delta$ and $O$ on the other side of $a$ than $A$. The angles between $S$ and $b$, $c$ are $\beta$ and $\gamma$, resp. Now, construct a circle $S_0$ centered in $A$ which intersects $S$ orthogonally. Scaling this construction such that the second circle has radius $1$ yields a triangle with the prescribed angles in the Poincaré model.

Theorem.
The area of a hyperbolic triangle with angles $\alpha$, $\beta$, $\gamma$ is $\pi-(\alpha+\beta+\gamma)$.

Proof.
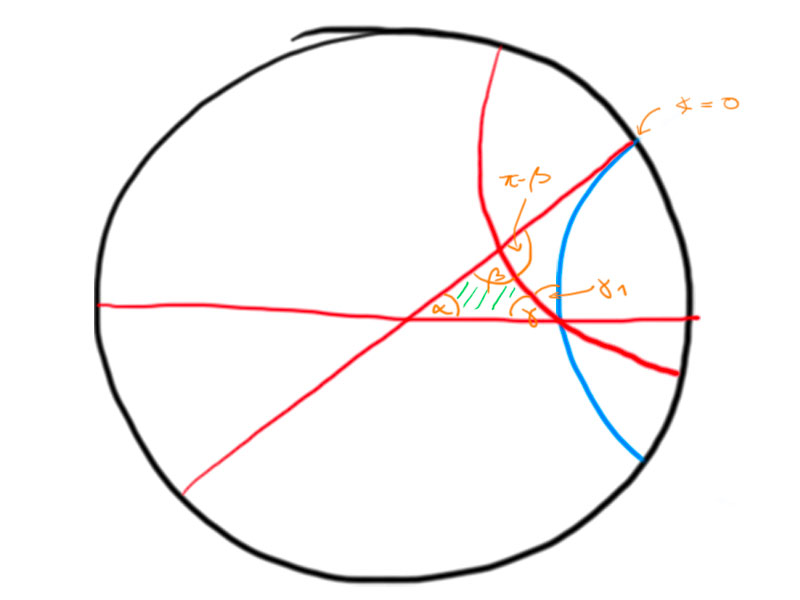
Consider a triangle with one point at infinity, i.e. on the boundary of the disc in the Poincaré model.

We may normalize the picture and transform it to the upper half-plane model, such that we obtain the following picture:

The area of the triangle is
\begin{align*}
T(\alpha,\beta,0)&=\int_{-\cos\alpha}^{\cos\beta}\int_{\sqrt{1-x^2}}^\infty\frac1{y^2}\mathrm dy\mathrm dx \\
&=\int_{-\cos\alpha}^{\cos\beta}-\left.\frac1y\right\vert_{\sqrt{1-x^2}}^\infty\mathrm dx \\
&=\int_{\cos(\pi-\alpha)}^{\cos\beta}\frac1{\sqrt{1-x^2}}\mathrm dx \\
&=\pi-(\alpha+\beta)\,.
\end{align*}

Now,
\begin{align*}
T(\alpha,\beta,\gamma)&=T(\alpha,\gamma+\gamma_1,0)-T(\gamma_1,\pi-\beta,0) \\
&=\pi-\alpha-\gamma-\gamma_1-(\pi-\gamma_1-\pi+\beta)\\
&=\pi-(\alpha+\beta+\gamma)\,.
\end{align*}

Proposition
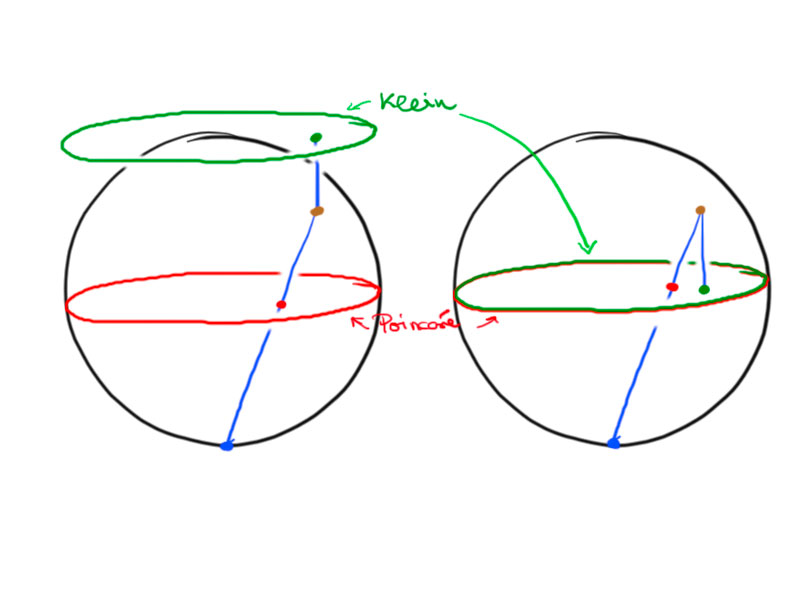
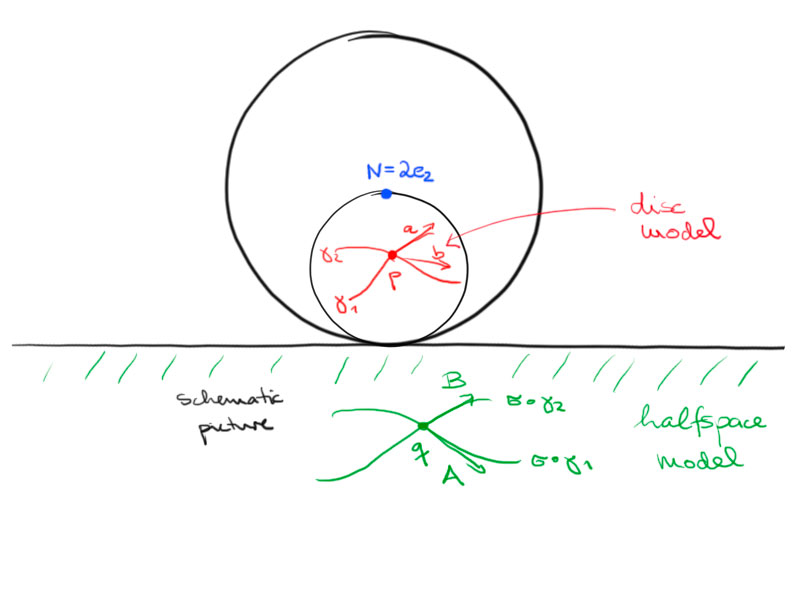
We can identify the Poincaré and the Klein model by the following construction:
Consider the Klein and Poincaré disc and embed it in $\R^3$ at $x_3=0$ inside the unit sphere (cf. second picture).

To obtain a point in the Poincaré model from a point in the Klein model, we do the following:

1. Project vertically, along $e_3$, onto the upper hemisphere.
2. Use the stereographic projection from $-e_3$ (south pole) to project the upper

hemisphere back onto the disc.

Corollary
The geodesics in the Poincaré model are circular arcs (or line segments through the origin) that intersect the unit sphere/circle orthogonally.

Proof.
In the Klein model geodesics are secants. They are mapped to semicircles that intersect the boundary (the equator) orthogonally in the hemisphere.
Since the steographic projection is conformal and maps circles (or lines) to circles (or lines) the geodesics in the Poincaré disc are circular arcs that intersect the unit circle orthogonally.

Example.
For two lines construct the unique perpendicular.

Remark.
On the way we constructed another conformal model of the hyperbolic space on the hemisphere.

The Poincaré half-space(/-plane) model

Consider the following map:

\[\sigma\colon x\mapsto\sigma(x)=2e_2+\frac4{(x-2e_2,x-2e_2)}(x-2e_2)\,.\]
We have $\sigma(S^1+e_2)=(\R\times\{0\})\cup\infty$.
Further, $\sigma(D+e_2)=H_-^2$, where $H_-^2:=\{(x,y)^{\mathrm T}\in\R^2:y<0\}$.
By a similar calculation as the one in the proof of conformality of the Poincaré model we can show the following:

\[(A,B)=\frac{16}{(p-e,p-e)^2)}(a,b)\]
by considering the map
\[\tilde\sigma\colon D\to H_1^2\,,\ p\mapsto2e_2+\frac4{(p-e_2,p-e_2)}(p-e_2)=\sigma(p+e_2)\,.\]
For the hyperbolic metric on the Poincaré model we had
\[g_p(a,b)=\frac4{(1-(p,p))^2}(a,b)=\frac{4(p-e_2,p-e_2)^2}{16(1-(p,p))^2}(A,B)=\frac1{q_2^2}(A,B)\,,\]
where $q=\tilde\sigma(p)$.

Definition
The upper half space $H_+^n:=\{x\in\R^n:x_n>0\}$ endowed with the Riemannian metric
\[g_q(A,B)=\frac1{q_n^2}(A,B)\]
where $q\in H_+^n$ and $A,B$ are tangent vectors to $H_+^n$ at $q$ is the \emph{Poincaré half-space model} of the hyperbolic space.

Properties:
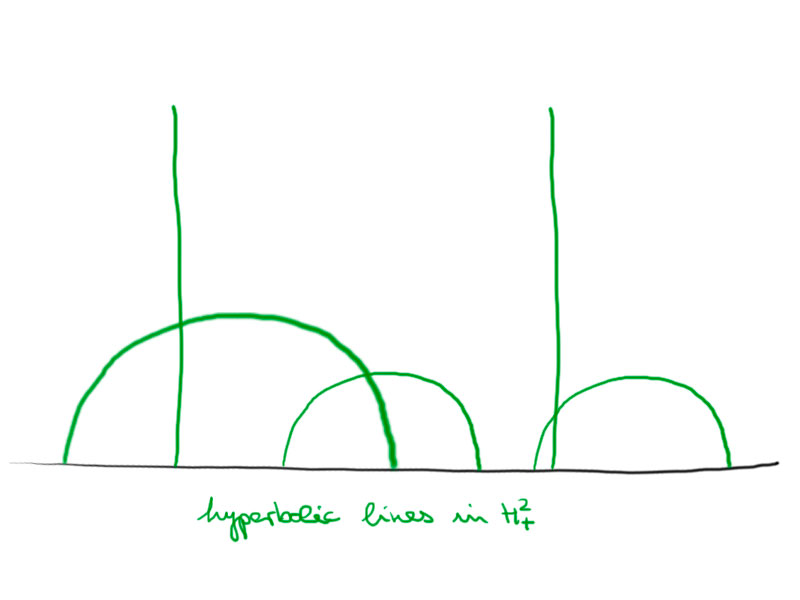
This model is conformal, i.e. the angles between curves correspond to the Euclidean angles.
The geodesics are semi-circles or lines that intersect the boundary orthogonally.

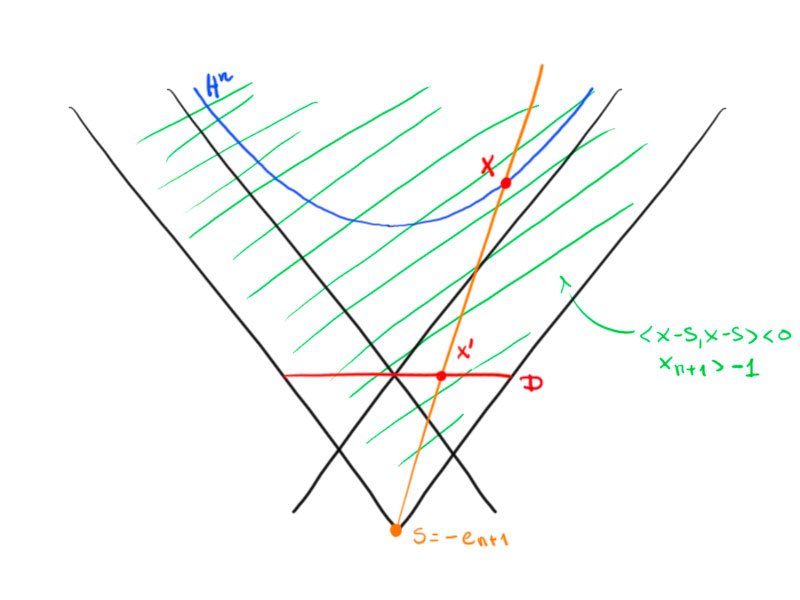
Poincaré disc/ball model

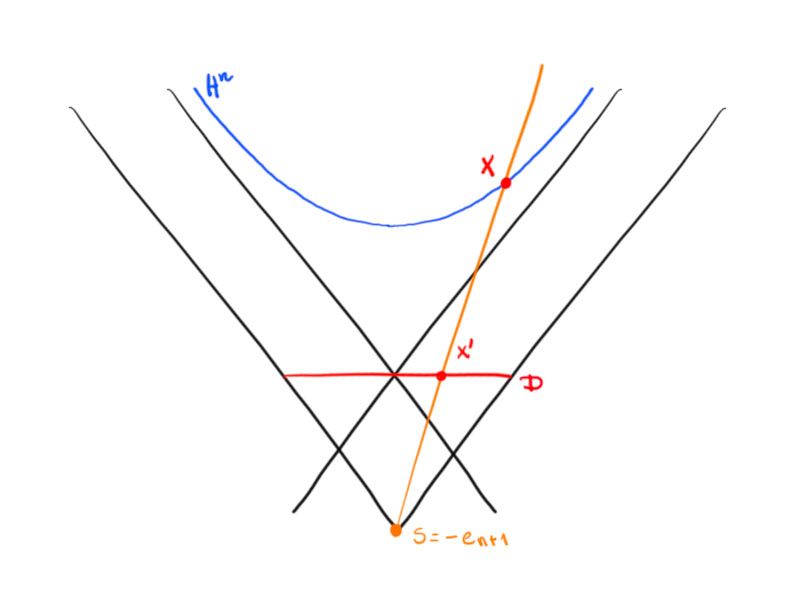
Consider the central projection with center $s$ of $H^n$ onto the plane $x_{n+1}=0$.
This map can be described by
\begin{align*}\sigma\colon H^n
&\to D=\{u\in\R^n:(u,u)<1\}\\
x&\mapsto\frac1{x_{n+1}+1}\begin{pmatrix} x_1\\\vdots\\x_n\end{pmatrix}\,.
\end{align*}
The inverse is given by
\[\sigma^{-1}(u)=\frac1{1-(u,u)}\begin{pmatrix} 2u\\1+(u,u)\end{pmatrix}\,.\]
For $s+t\left(\begin{pmatrix}u\\ 0\end{pmatrix}-s\right)=\begin{pmatrix}tu\\-1+t\end{pmatrix}$ is a point on $\vec{su}$ and
\[-1=\left\langle \begin{pmatrix}tu\\-1+t\end{pmatrix},\begin{pmatrix}tu\\-1+t\end{pmatrix}\right\rangle_{n,1}=t^2(u,u)-(t-1)^2=t^2(u,u)-t^2+2t-1\]
yields $t=0$ or $t(u,u)+2-t=0$ which is equivalent to $t=\frac2{1-(u,u)}$.
This implies $X=\begin{pmatrix}\frac2{1-(u,u)}u\\-1+\frac2{1-(u,u)}\end{pmatrix}=\frac1{1-(u,u)}\begin{pmatrix} 2u\\1+(u,u)\end{pmatrix}$.

The map $\sigma$ is the restriction of the following map to $H^n$:
\[x\mapsto s-\frac2{\langle x-s,x-s\rangle_{n,1}}(x-s)\,,\quad\text{for}\ \langle x-s,x-s\rangle_{n,1}\neq0\,.\]

A point $x$ with $\langle x-s,x-s\rangle<0$ is mapped to a point on the ray $\vec{sx}$.

The plane $x_{n+1}=0$ is the orthogonal complement of $s$:
\begin{align*}\left\langle s-\frac2{\langle x-s,x-s\rangle}(x-s),s\right\rangle&=\langle s,s\rangle-\frac{2\langle x-s,s\rangle}{\langle x-s,x-s\rangle}=-1-\frac{2(\langle x,s\rangle-\langle s,s\rangle)}{\langle x,x\rangle-2\langle x,s\rangle+\langle s,s\rangle}\\&=-1-\frac{2(\langle x,s\rangle+1)}{-2-2\langle x,s\rangle}=0\,.\end{align*}
This map is an involution on the set $\{x\in\R^{n,1}:\langle x-s,x-s\rangle-1\}$ with $\sigma(H^n)=D$ and $\sigma(D)=H^n$, where $D\cong D\times\{0\}$.

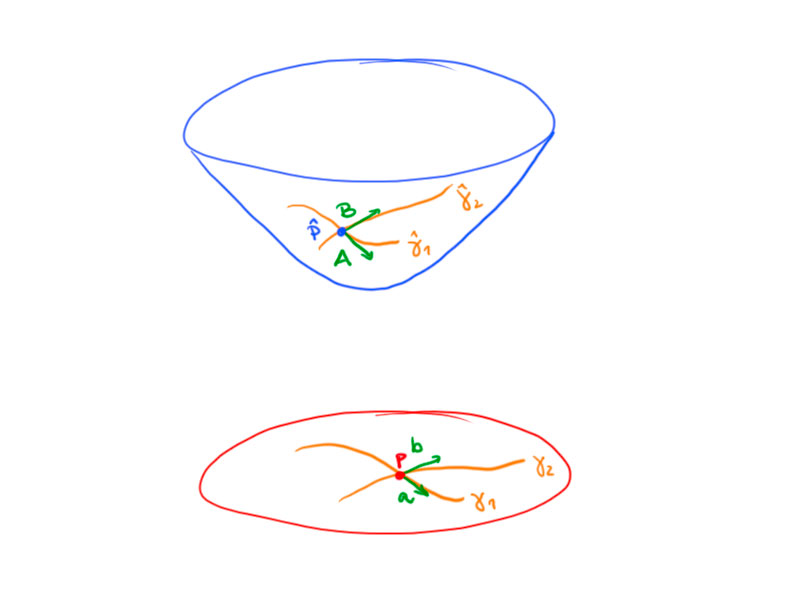
Theorem.
Consider two curves $\gamma_1,\gamma_2\subseteq D$ with $\gamma_1(0)=\gamma_2(0)=p\in D$ and $a:=\gamma_1′(0)$, $b:=\gamma_2′(0)$.
Let $\hat\gamma_1:=\sigma\circ\gamma_1$ and $\hat\gamma_2:=\sigma\circ\gamma_2$ be the corresponding curves in $H^n$ with $\hat\gamma_1(0)=\hat\gamma_2(0)=P=\sigma(p)$ and $A:=\hat\gamma_1′(0)$, $B:=\hat\gamma_2′(0)$.
Then:
\[\langle A,B\rangle_{n,1}=\frac4{(1-(p,p))^2}(a,b)\,.\]
This implies
\[\cosh\alpha=\frac{\langle A,B\rangle}{\sqrt{\langle A,A\rangle\langle B,B\rangle}}=\frac{(a,b)}{\sqrt{(a,a)(b,b)}}\,,\]
where $\alpha$ is the angle of intersection of $\hat\gamma_1$ and $\hat\gamma_2$.

Proof.
Calculate derivatives:
\[A=\hat\gamma_1′(0)=\frac{\mathrm d}{\mathrm dt}\left.\left(s-\frac2{\langle \gamma_1(t)-s,\gamma_1(t)\rangle}(\gamma_1(0)-s)\right)\right\vert{t=0}=-2\frac a{\langle p-s,p-s\rangle}+2\frac{2\langle p-s,a\rangle}{\langle p-s,p-s\rangle^2}(p-s)\,.\]
Similarly,
\[B=-2\frac b{\langle p-s,p-s\rangle}+2\frac{2\langle p-s,b\rangle}{\langle p-s,p-s\rangle^2}(p-s)\,.\]
Now,
\begin{align*}\langle A,B\rangle
&=\frac{4\langle a,b\rangle}{\langle p-s,p-s\rangle^2}-{2\cdot8\frac{\langle p-s,a\rangle\langle p-s,b\rangle}{\langle p-s,p-s\rangle^3}}+{16\frac{\langle p-s,a\rangle\langle p-s,b\rangle\langle p-s,p-s\rangle}{\langle p-s,p-s\rangle^4}}\\&=\frac4{(\langle p,p\rangle-2\langle p,s\rangle+\langle s,s\rangle)^2}(a,b)=\frac4{((p,p)-1)^2}(a,b)\,.\end{align*}

Definition
The open unit ball $D=\{u\in\R^n:(u,u)<1\}$ endowed with the \emph{Riemannian metric}
\[g_u(a,b)=\frac4{(1-(u,u))^2}(a,b)\,,\]
where $a$, $b$ are tangent vectors to $D$ at $u$, is the \emph{Poincaré ball model} of the hyperbolic space.
It is \emph{conformal}, i.e. the hyperbolic angles equal the Euclidean angles.

The \emph{length of a curve $\gamma\colon[0,1]\to D$} is given by
\[\operatorname{length}(\gamma)=\int_0^1\sqrt{g_{\gamma(t)}(\gamma'(t),\gamma'(t))}\mathrm dt\,.\]

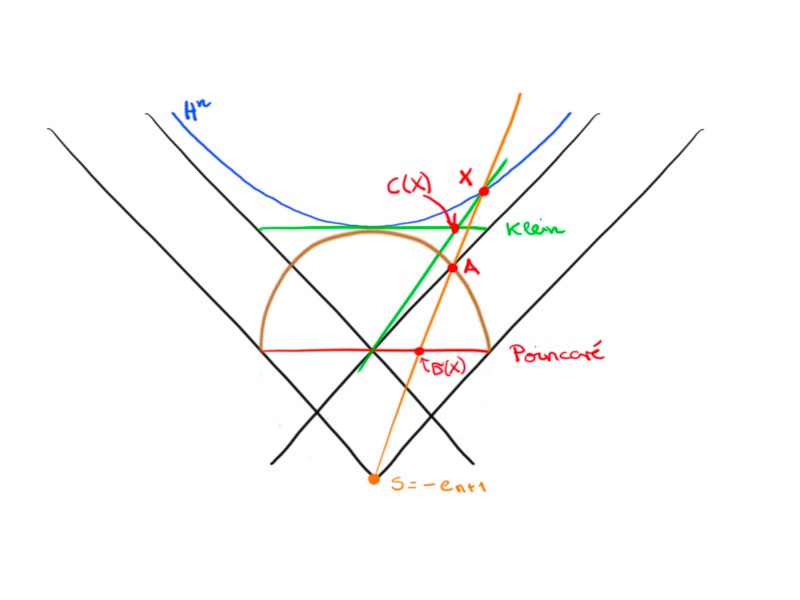
Relation between Klein and Poincaré model

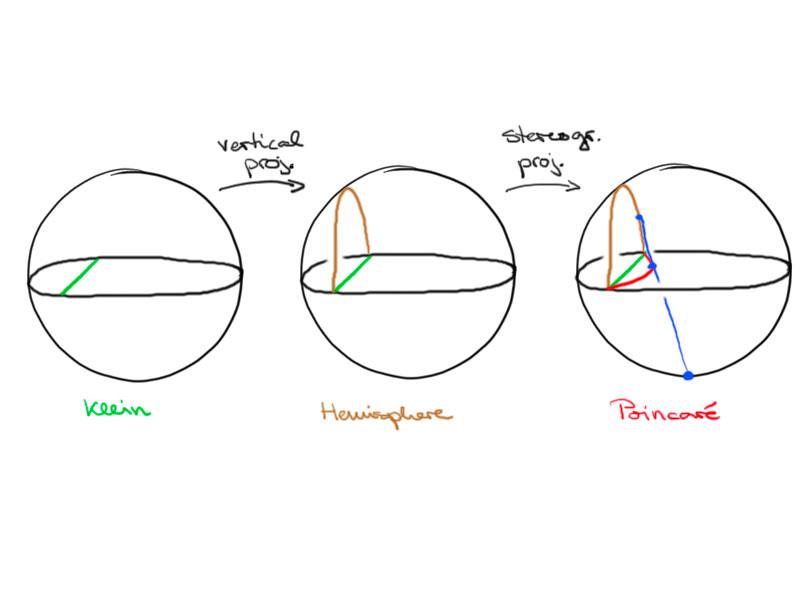
Claim: $A$ is the vertical projection along $e_{n+1}$ of $c(x)$ onto the hemisphere:
\[A_i=c(x)_i\quad\text{for all}\ i=1,\dotsc,n\,.\]
For this, observe that $A=s+t(x-s)$ for some $t$ and $(A,A)=1$.
Thus $\left(s+t\begin{pmatrix} x_1\\\vdots\\x_{n+1}+1\end{pmatrix},s+t\begin{pmatrix} x_1\\\vdots\\x_{n+1}+1\end{pmatrix}\right)=1$ yields
\[1=1+2\left(s,t\begin{pmatrix} x_1\\\vdots\\x_{n+1}+1\end{pmatrix}\right)+t^2\left\lVert\begin{pmatrix} x_1\\\vdots\\x_{n+1}+1\end{pmatrix}\right\rVert^2\]
and hence
\[0=-2t(x_{n+1}+1)+t^2\left(\sum_{i=1}^nx_i^2+x_{n+1}^2+2x_{n+1}+1\right)\,.\]
Now by $\langle x,x\rangle=-1$ we obtain
\[t^2\sum_{i=1}^nx_i^2=t^2(x_{n+1}^2-1)\]
which gives us $t=0$ or
\[t=\frac{2(x_{n+1}+1)}{2x_{n+1}(x_{n+1}+1)}=\frac1{x_{n+1}}\,.\]
So $A=\begin{pmatrix}0\\-1\end{pmatrix}+\frac1{x_{n+1}}\begin{pmatrix} x\\x_{n+1}+1\end{pmatrix}\in\R^{n,1}$.
Thus
\[(A)_{i=1,\dotsc,n}=\frac1{x_{n+1}}x\,.\]
The coordinates of $c(x)$ are given by
\[c(x)=\begin{pmatrix}\frac1{x_{n+1}}x\\1\end{pmatrix}\,.\]
This proves the claim.

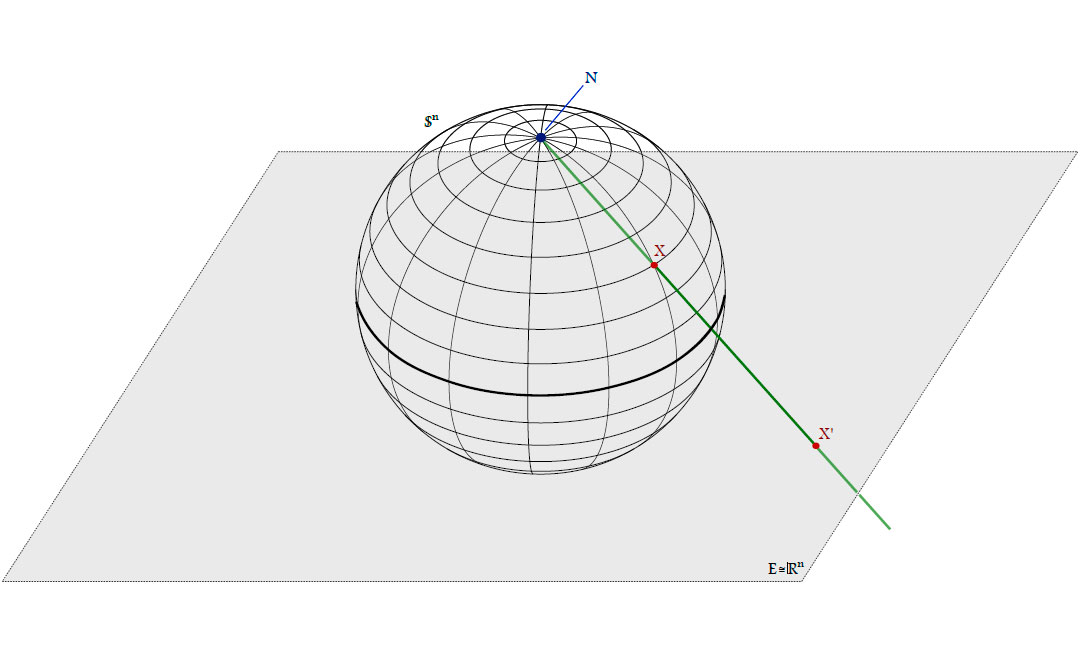
Stereographic projection

Definition. Denote the unit sphere in $\mathbb{R}^{n+1}$ by $\mathbb{S}^{n}=\left\{{x \in \mathbb{R}^{n+1}|(x,x)=1}\right\}$ and its north pole by $\mathbf{N}=e_{n+1}$.
The stereographic projection is a map $\sigma\colon \mathbb{S}^{n}\to\mathbb{R}^{n} \cup \left\{{\infty}\right\}$ from $\mathbf{N}$ to the plane
$E=\left\{{x \in \mathbb{R}^{n+1}|x_{n+1}=0}\right\} \cong \mathbb{R}^{n}$ through the equator:
\[
\sigma(X)=
\left\{
\begin{array}{ll}
\infty & \textrm{, } X = \mathbf{N}\\
l_{NX}\cap E & \textrm{, } X \neq \mathbf{N}\\
\end{array}
\right.
\]
Analytically $\sigma$ is given by
\[
\sigma(X)= \sigma\ \left(\begin{pmatrix}
x_1\\\vdots\\x_{n+1}
\end{pmatrix} \right)
= \frac{1}{1-x_{n+1}}\begin{pmatrix}
x_1\\\vdots\\x_{n+1}
\end{pmatrix}
\]
since
\[N+\lambda(X-N)=e_{n+1}+\lambda \begin{pmatrix}
x_1\\\vdots\\x_{n+1}
\end{pmatrix}
= \begin{pmatrix}
y_1\\\vdots\\y_{n}\\0
\end{pmatrix}
\Rightarrow \lambda=-\frac{1}{x_{n+1}-1}=\frac{1}{1-x_{n+1}}, X\neq N.
\]

Sphere inversion
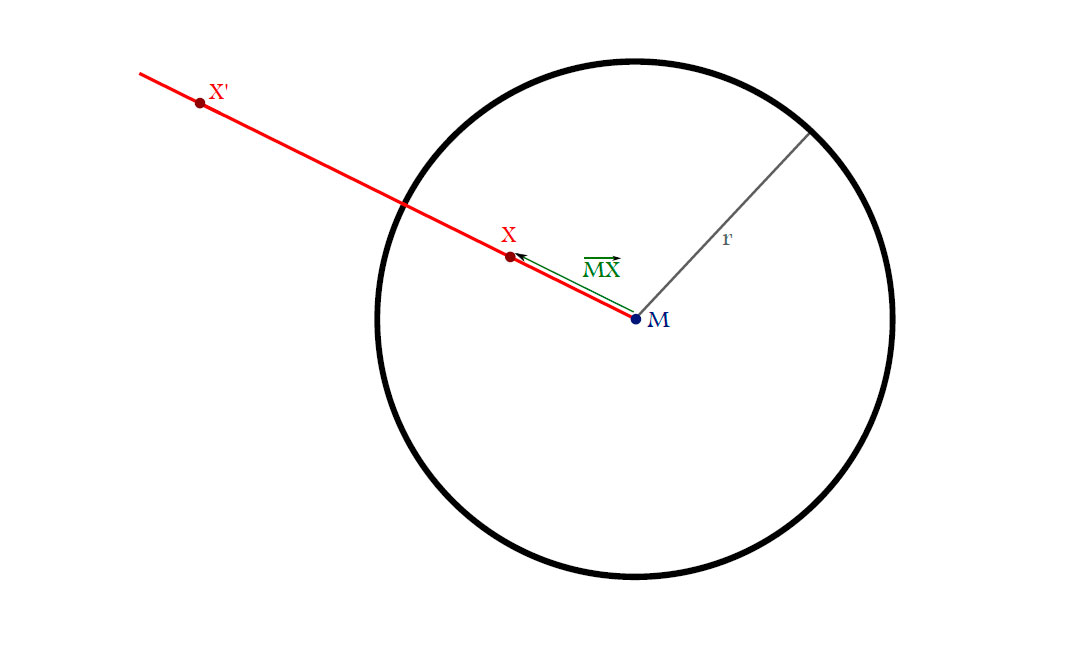
Definition. The sphere inversion $i_{M,r}\colon \mathbb{R}^{n} \cup \left\{{\infty}\right\} \to \mathbb{R}^{n} \cup \left\{{\infty}\right\}$ in the sphere
$\mathbf{S}_{M,r}=\left\{{x \in \mathbb{R}^{n}|\left\|x-M\right\|=r}\right\}$ is given by the following conditions:

• $X’$ lies on the ray $\overrightarrow{MX}$,
• $\left\|M-X\right\|\left\|M-X’\right\|=r^2$,
• $M\longleftrightarrow\infty$.

Properties of sphere inversions

1. $i_{M,r}$ is an involution,
2. $\mathbf{S}_{M,r}$ is fixed,
3. affine subspaces containing M are mapped onto themselves.

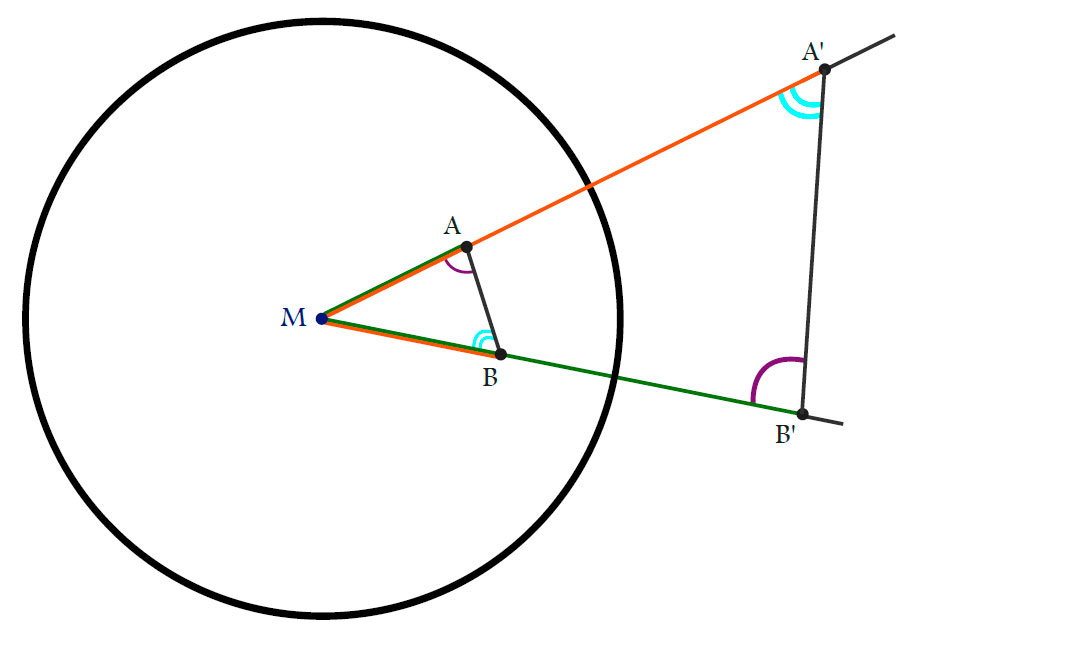
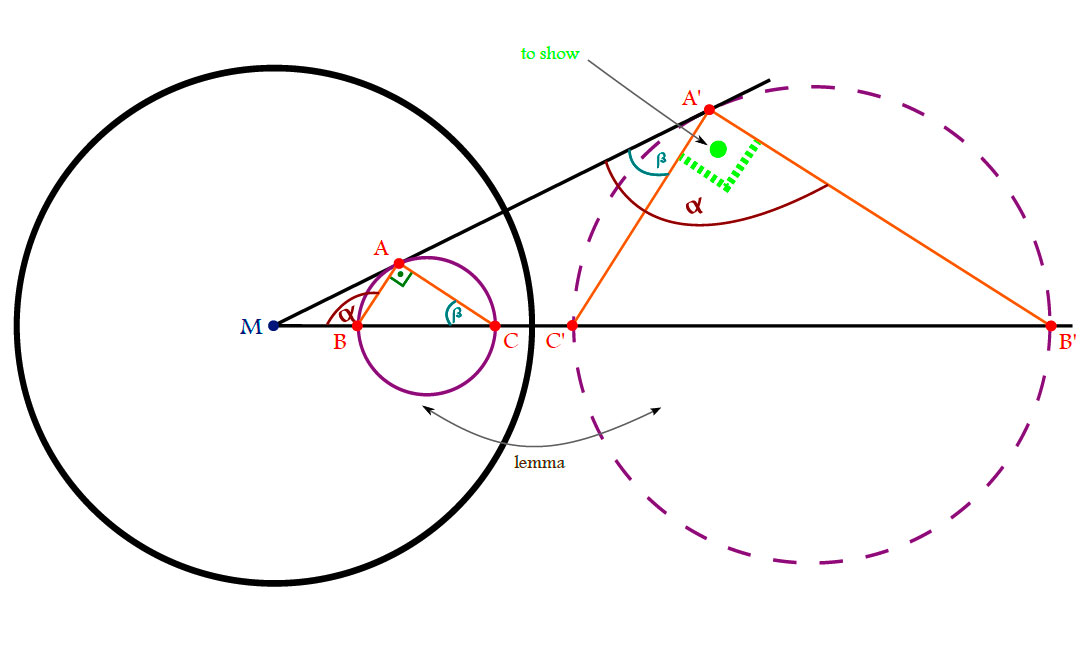
Lemma.

Proof.
Since
\[
\left\|M-A\right\|\left\|M-A’\right\|=r^2 = \left\|M-B\right\|\left\|M-B’\right\| \iff
\frac{\left\|M-A\right\|}{\left\|M-B\right\|}=\frac{\left\|M-B’\right\|}{\left\|M-A’\right\|}
\]
we get that $\Delta AMB$ and $\Delta B’MA’$ are similar. In particular:
\[
\measuredangle MA’B’=\measuredangle ABM.
\measuredangle MAB=\measuredangle A’B’M.
\]

$\Box$

Corollary. Circles through M are mapped to lines. In particular, the line is parallel to the tangent to the circle at M.

Remark. All lines are thought to contain the point $\infty$ and are considered as circles of infinte radius.

Corollary. The stereographic projection is the restriction of the sphere inversion $i_{M,r}$ with $M=e_{n+1}$ and $r=\sqrt{2}$.

Proof.

1. The equator of $\mathbb{S}^{n}$ is fixed.
2. $\mathbb{S}^{n}$ is mapped to a plane (Corollary) through the equator (1).
3. Both inversion and stereographic projection preserve the rays.
4. The intersection points of a ray with $\mathbb{S}^{n}$ and $\mathbb{R}^{n}$ are unique, hence $i_{M,r}\Big|_{\mathbb{S}^{n}}=\sigma$.
5. $N=M\longrightarrow\infty$ by $i_{M,r}$.

$\Box$

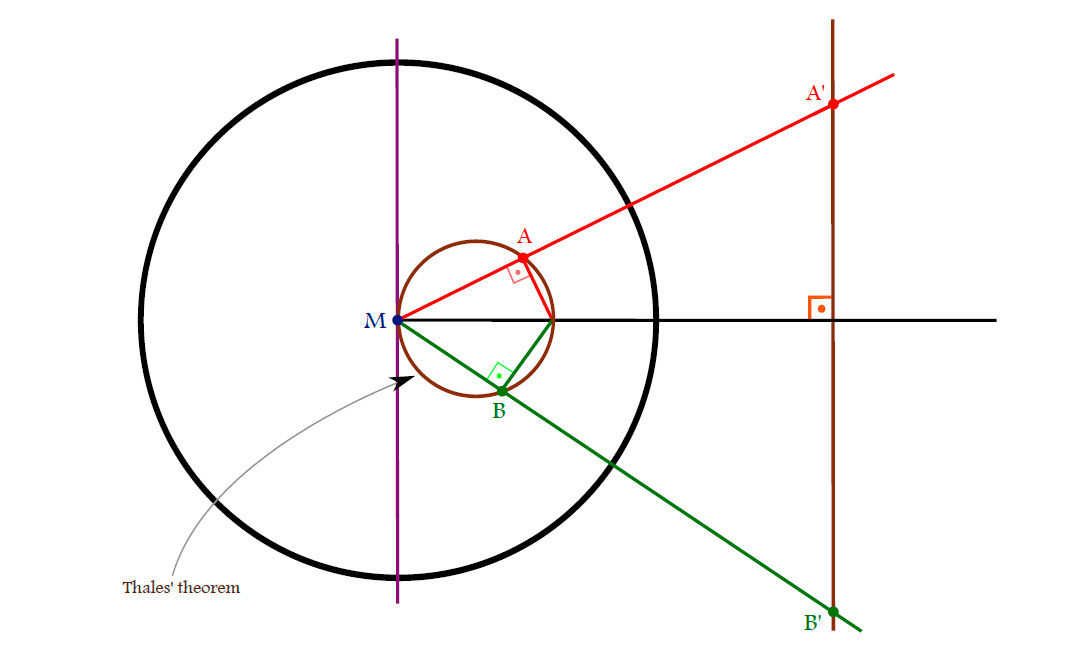
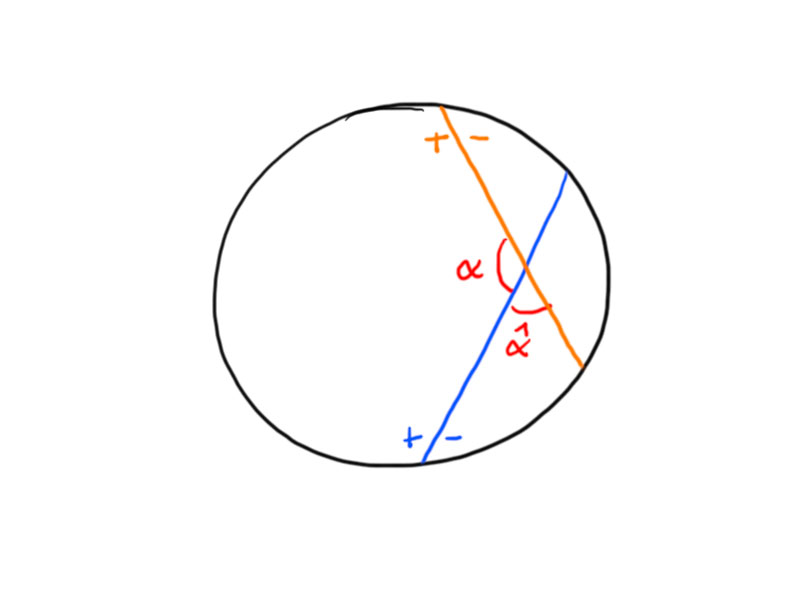
Theorem. An inversion in a sphere:

1. maps spheres/hyperplanes to spheres/hyperplanes,
2. is a conformal map, i.e. it preserves angles.

Proof.
(i) Consider the following sketch:

Hence the angles $\alpha$ and $\beta$ satisfy
\[
(\pi-\alpha)+\beta+\frac{\pi}{2}=\pi \Rightarrow \alpha-\beta=\frac{\pi}{2}.
\]
(ii) Conformality follows from the following picture

$\Box$

Remark. In general, the center of a sphere is not mapped to the center of its image by an inversion.

Corollary.

1. The stereographic projection maps spheres through the north pole to hyperplanes and spheres not through the north pole to spheres.
2. All spheres/hyperplanes are images of spheres on $\mathbb{S}^{n}$ under $\sigma$ (because $i_{0,1}$ is an involution).
3. $\sigma$ is conformal.

Formula for the sphere inversion.
Consider the second figure showing the general idea of a sphere inversion. Since $X’$ lies on the ray $XM$ we have $X’=M+\lambda(X-M), \lambda > 0$ and from the second requirement for the sphere inversion we obtain

\begin{align*}
&&\underbrace{\left\|X’-M\right\|}_{X’-M=\lambda(X-M)} \left\|X-M\right\|&=r^2\\
\Rightarrow&& \lambda \left\|X-M\right\| \left\|X-M\right\|&=r^2\\
\Rightarrow&& \lambda = \frac{r^2}{\left\|X-M\right\|^2}.
\end{align*}
Hence the sphere inversion is given by

\[
i_{M,r}=M+\frac{r^2}{\left\|X-M\right\|^2}(X-M).
\]

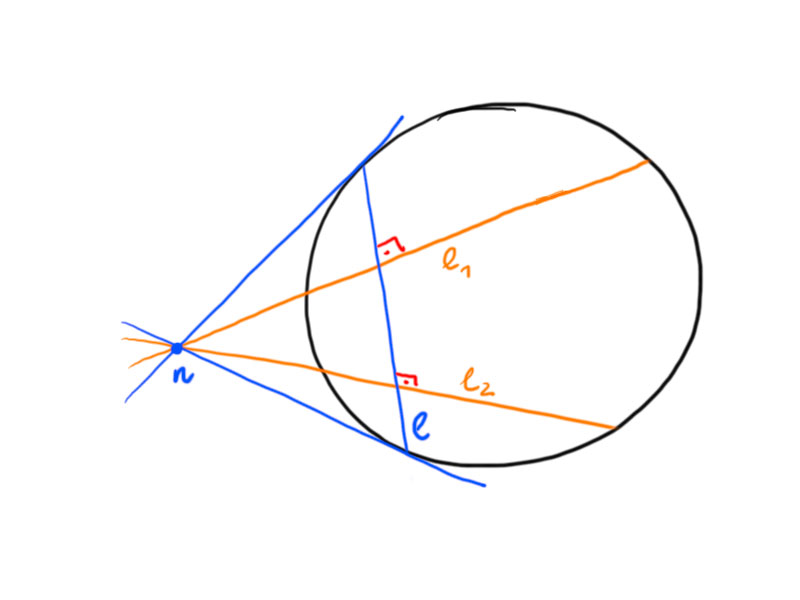
Definition.
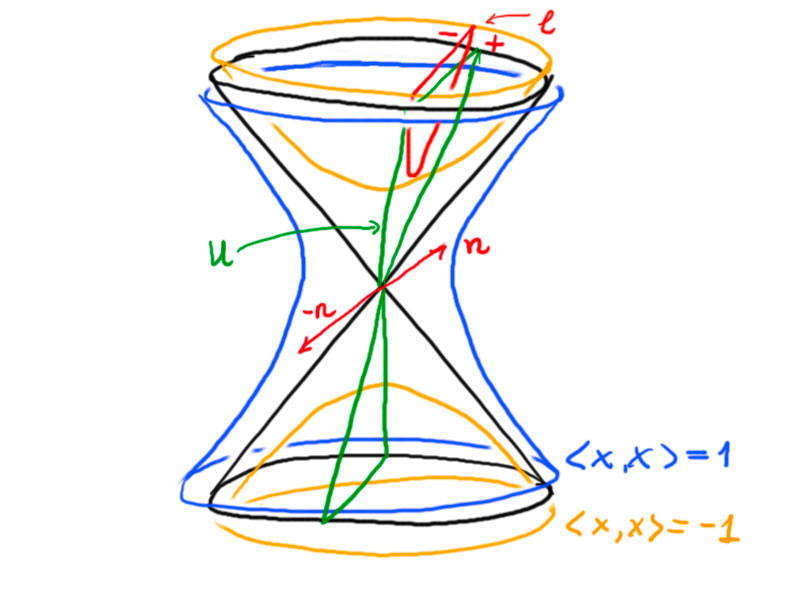
Let $\ell_1$, $\ell_2$ be two intersecting lines defined by unit normals $n_1$, $n_2$.
The exterior angle $\hat\alpha$ of these two lines is given by
\[\cos\hat\alpha=\langle n_1,n_2\rangle\,.\]
The interior angle $\alpha=\pi-\hat\alpha$ is given by
\[\cos\alpha=-\langle n_1,n_2\rangle\,.\]

In particular, two lines are perpendicular, if $\langle n_1,n_2\rangle=0$.

Remark.
The Euclidean angle of intersection differs from the hyperbolic angle defined above.

Example
I don’t remember the example 🙁

Proposition

1. Given $x\in H^2$ and a line $\ell\subset H^2$, there exists a unique line through $x$ perpendicular to $\ell$.
2. If $\ell_1,\ell_2\in H^2$ are two non-intersecting lines ($\lvert \langle n_1,n_2\rangle\rvert >1$), then there exists a unique line perpendicular to $\ell_1$ and $\ell_2$.

Proof. Homework.

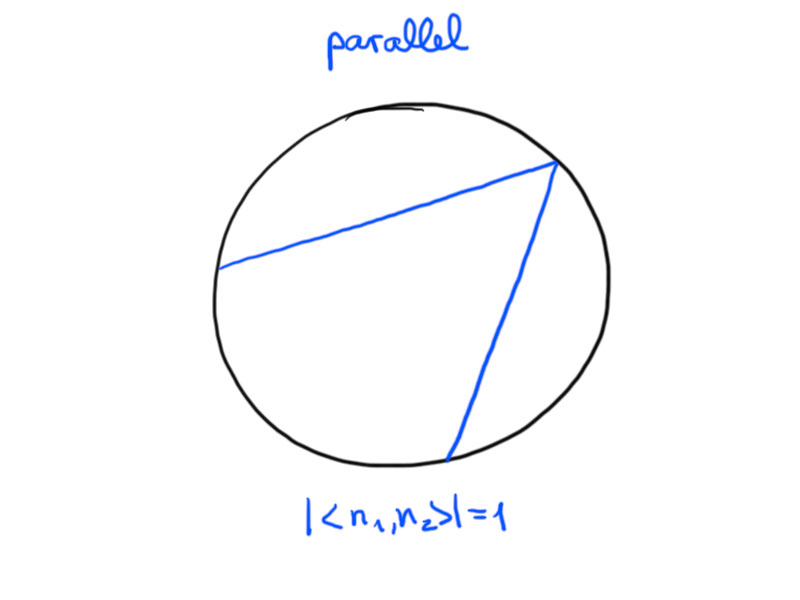
Let $\ell_1,\ell_2\in H^2$ be two hyperbolic lines with unit normal vectors $n_1$, $n_2$:

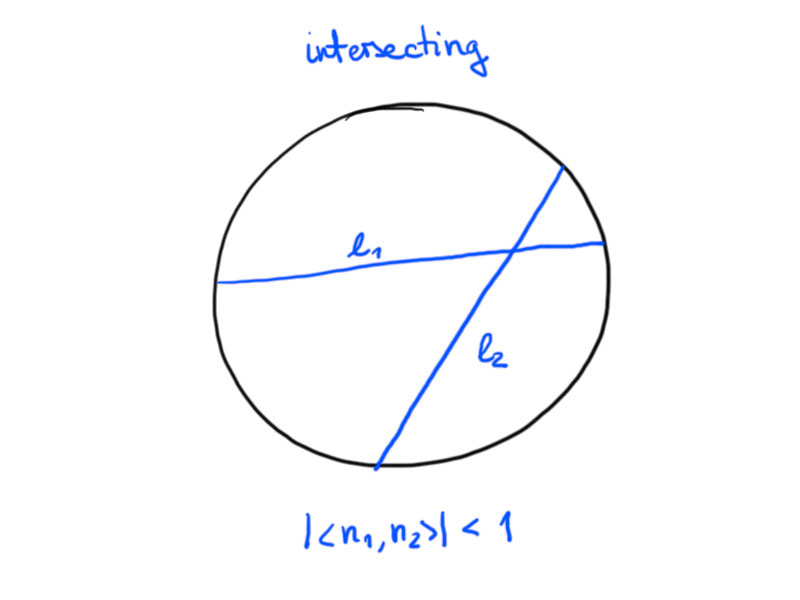
If $\lvert \langle n_1,n_2\rangle\rvert < 1$, then $\ell_1$ and $\ell_2$ intersect.

If $\lvert \langle n_1,n_2\rangle\rvert = 1$, we call $\ell_1$ and $\ell_2$ parallel.

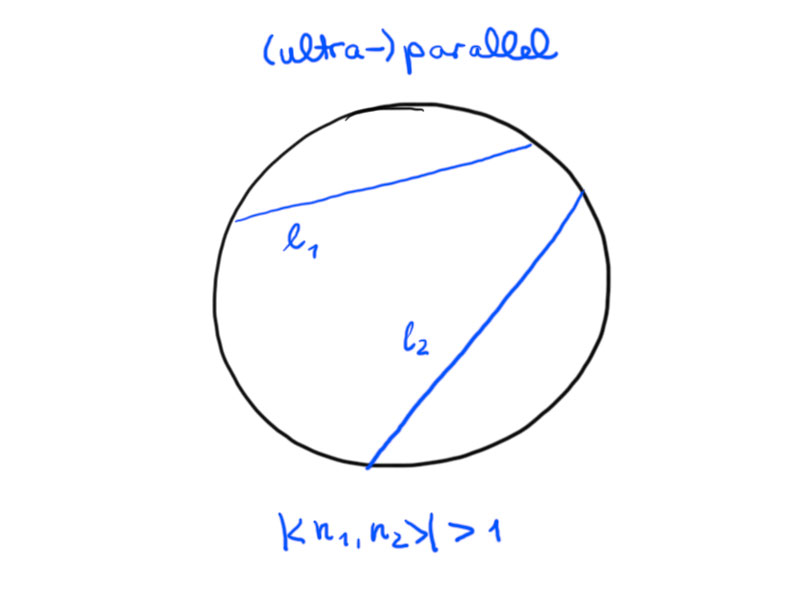
If $\lvert \langle n_1,n_2\rangle\rvert >1$, we call $\ell_1$ and $\ell_2$ (ultra-)parallel.

Distances in the hyperbolic plane

Proposition
The point on a line $\ell\subset H^2$ closest to a point $x\in H^2$ is the intersection point of $\ell$ with its unique perpendicular line through $x$.

Proof.

W.l.o.g. assume $x\notin\ell$.
We have
\begin{align*}
\langle n_p,x\rangle&=\langle n_p,x_p\rangle=0&
\langle n,x_p\rangle&=0&
\langle n_p,n\rangle&=0\,.
\end{align*}
We normalize $n_p$ and $x_p$ such that $\langle n_p,n_p\rangle=1$ and $\langle x_p,x_p\rangle=-1$.
Now $\gamma(s)=\cosh(s)x_p+\sinh(s)n_p$ is an arclength parametrization of $\ell$.
The distance from $x$ to $\gamma(s)$ is
\[\cosh d(x,\gamma(s))=-\langle x,\gamma(s)\rangle=-\langle x,\cosh(s)x_p\rangle-\langle x,\sinh(s)n_p\rangle=-\cosh(s)\langle x,x_p\rangle\,.\]
This is minimal for $s=0$, $\gamma(0)=x_p$.
Thus the closest point is $x_p$.

Proposition

1. For the distance of a point $x\in H^2$ to a line $\ell\subset H^2$ defined by a unit normal $n$, we have
   \[\sinh d(x,\ell)=\lvert \langle x,n\rangle\rvert \,,\]
   where $d(x,\ell)=d(x,x_p)$ and $x_p$ is closest to $x$ on $\ell$.
2. The distance between two non-intersecting lines $\ell_1,\ell_2\subset H^2$ with unit normals $n_1$, $n_2$ is
   \[\cosh d(\ell_1,\ell_2)=\lvert \langle n_1,n_2\rangle\rvert\,,\]
   where $d(\ell_1,\ell_2)$ is the minimal distance of two points on $\ell_1$, $\ell_2$, resp., or $d(\ell_1,\ell_2)=d(x_1,x_2)$, where $x_i=\ell_i\cap\ell_p$ and $\ell_p\perp\ell_1,\ell_2$.

Proof.
(i). Consider the arclength parametrization
\[\gamma_p(s)=\cosh(s)x_p+\sinh(s)n\]
of $\ell_p$.

Now
\[x=\gamma_p(s_0)\quad\text{with}\quad s_0=\pm d(x,x_p)\,.\]
Thus
\[\lvert \langle n,x\rangle\rvert =\lvert \langle n,\cosh(s_0)x_p+\sinh(s_0)n\rangle\rvert =\lvert \sinh(s_0)\rvert \,,\]
as $n$ is normalized to $\langle n,n\rangle=1$.
This yields
\[\sinh d(x,\ell)=\sinh d(x,x_p)=\lvert \langle n,x\rangle\rvert \,.\]

(ii). Parametrize $\ell_1$ as follows:
\[\gamma_1(s)=\cosh(s)x_1+\sinh(s)n_p\,.\]
The distance of $\gamma_1(s)$ to $\ell_2$ is
\[\sinh d(\gamma(s),\ell_2)=\lvert \langle \gamma_1(s),n_2\rangle\rvert =\cosh(s)\lvert \langle x_1,n_2\rangle\rvert \]
since $\langle n_2,n_p\rangle=0$.
This is minimal for $s=0$, i.e. $x_1$ is closest to $\ell_2$ on $\ell_1$
Similarly, $x_2$ is the point closest to $\ell_1$ on $\ell_2$.
Now parametrize $\ell_p$.
\begin{align*}
x_1&=\cosh(s_0)x_2+\sinh(s_0)n_2&
x_2&=\cosh(\tilde s_0)x_1+\sinh(\tilde s_0)n_1\,.
\end{align*}
Here, $s_0=\pm d(x_1,x_2)=\pm\tilde s_0$.
Thus with $\langle n_1,n_1\rangle=1$
\begin{align*}0
&=\langle n,x_1\rangle=\cosh(s_0)\langle n_1,x_2\rangle+\sinh(s_0)\langle n_1,n_2\rangle=\cosh(s_0)\sinh(\tilde s_0)+\sinh(s_0)\langle n_1,n_2\rangle\\
&=\sinh(s_0)(\cosh(s_0)\pm\langle n_1,n_2\rangle)
\end{align*}
and hence $\cosh d(\ell_1,\ell_2)=\lvert \langle n_1,n_2\rangle\rvert $.

Intersections of $H^2$ with planes

Definition.
An affine plane is determined by one equation
\[\langle n,x\rangle_{2,1}=b\]
where $n\in\R^{2,1}$, $n\neq0$, and $b\in\R$.

Let $n$ be time-like, $\langle n,n\rangle < 0$.
If $\langle n,n\rangle=-1$, then $n\in H^2$ and $-\langle n,x\rangle=\cosh d(x,n)$ shall be equivalent to $\langle n,x\rangle=b$, i.e. the intersection of the plane given by $\langle n,x\rangle=b$ is a hyperbolic circle around $n$ with radius $r$ such that $\cosh r=-b$ ($b<0$).

What are the sets defined by space-like and isotropic normal vectors?

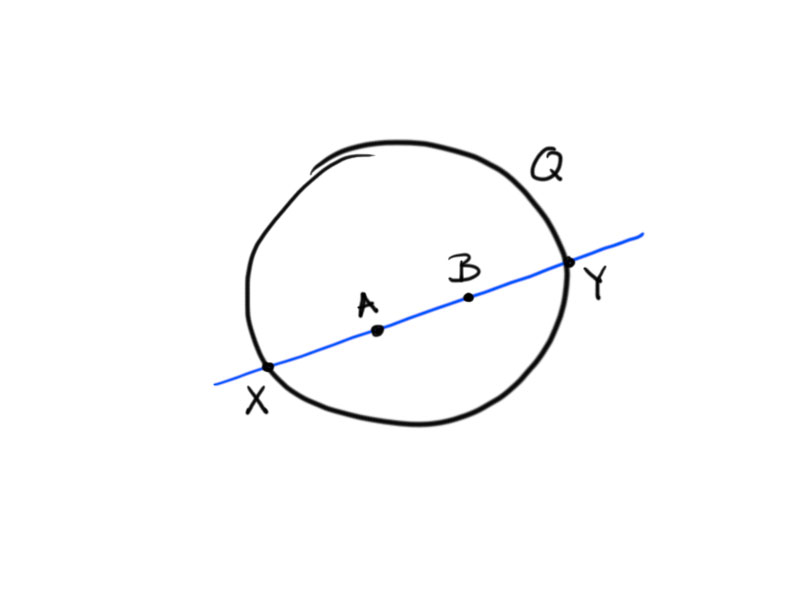
Theorem. For two points $A,B\in H_{\mathrm{pr}}^n$ let $X$, $Y$ be the points of intersection of the line $AB$ with the quadric $Q=\{[x]:\langle x,x\rangle_{n,1}=0\}$, such that $\{A,Y\}$ and $\{B,X\}$ separate each other.
Then
\[d_{\mathrm{pr}}(A,B)=\frac12\log\cr(B,X,A,Y)\,.\]

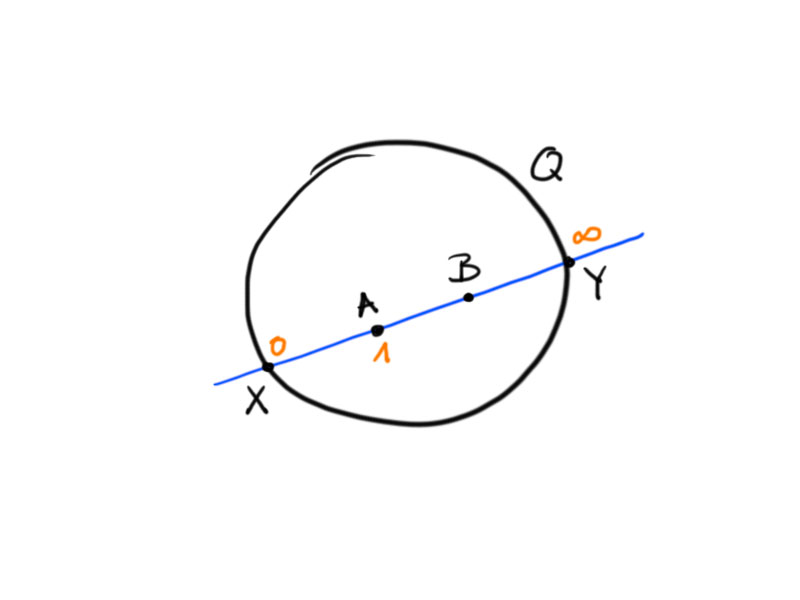
Proof.
Remember that $\cr(q,1,0,\infty)=q$.
If we choose an affine coordinate such that $X=0$, $A=1$ and $Y=\infty$, then we see that $\cr(B,X,A,Y)>1$, i.e. $\log\cr(B,X,A,Y)>0$.

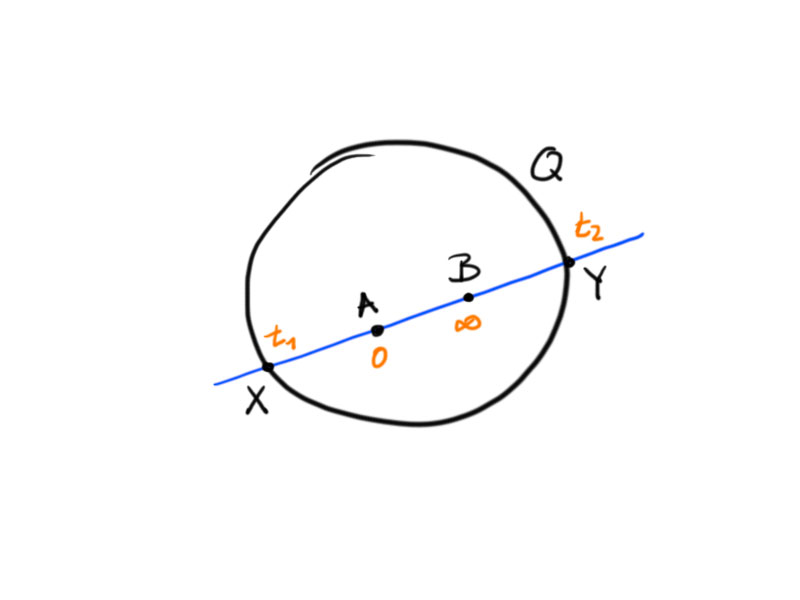
Parametrize $AB$ by $[a+tb]$ where $A=[a]$ and $B=[b]$.
Solving
\begin{equation}\langle a+tb,a+tb\rangle_{n,1}=0\label{ZeroesForXY}\end{equation}
yields the two solutions $t_1$, $t_2$ such that $X=[a+t_1b]$ and $Y=[a+t_2b]$.

We have $t_1t_2>0$ and: If $t_1,t_2>0$ then $t_2>t_1$, i.e. $\frac{t_2}{t_1}>1$ — if $t_1,t_2<0$ then $t_1>t_2$ and thus again $\frac{t_2}{t_1}>1$.
Looking back at the equation above gives us
\[0=\langle a+tb,a+tb\rangle=\langle b,b\rangle t^2+2t\langle a,b\rangle+\langle a,a\rangle=\langle b,b\rangle(t-t_1)(t-t_2)\,.\]
Comparing the coefficients yields
\begin{align*}
2\langle a,b\rangle&=-\langle b,b\rangle(t_1+t_2)&
\langle a,a\rangle&=\langle b,b\rangle t_1t_2\,,\quad
\text{i.e}\\
t_1+t_2&=-2\frac{\langle a,b\rangle}{\langle b,b\rangle}&
t_1t_2&=\frac{\langle a,a\rangle}{\langle b,b\rangle}\,.
\end{align*}
Thus
\[\cosh d_{\mathrm{pr}}(A,B)=\frac{\lvert\langle a,b\rangle\rvert}{\sqrt{\langle a,a\rangle\langle b,b\rangle}}=\frac{\lvert t_1+t_2\rvert}{2\sqrt{t_1+t_2}}\,.\]
The cross ratio is
\[\cr(B,X,A,Y)=\cr(\infty,t_1,0,t_2)=\frac{\infty-t_1}{t_1-0}\frac{0-t_2}{t_2-\infty}=\frac{t_2}{t_1}\,.\]
This implies
\begin{align*}\cosh\frac12\log\cr(B,X,A,Y)
&=\frac12\left(\mathrm e^{\frac12\log\frac{t_2}{t_1}}+\mathrm e^{-\frac12\log\frac{t_2}{t_1}}\right)=\frac12\left(\sqrt{\frac{t_2}{t_1}}+\sqrt{\frac{t_1}{t_2}}\right)\\
&=\frac12\frac{\lvert t_2\rvert+\lvert t_1\rvert}{\sqrt{t_1t_2}}=\frac12\frac{\lvert t_1+t_2\rvert}{\sqrt{t_1t_2}}\,,
\end{align*}
since $t_1t_2>0$.

Lines in the hyperbolic plane

Hyperbolic lines are secants of the unit ball

Obviously, to a line and a point in $H^2$ there exist many lines through the point that do not intersect the line:

This contradicts the Parallel Axiom.

Using polarity, we can assign unit normal vectors to hyperbolic lines in $H^2$.

With $\ell=P(U)$, where $U$ is a two-dimensional subspace with signature $(+-)$ (where by the signature of a subspace $V$ we denote the signature of $\langle\cdot\,,\cdot\rangle$ restricted to $V$) we have $n\in P(U^\perp)$, where $U^\perp$ has signature $(+)$ – so we can choose $n$ with $\langle n,n\rangle=1$.
For every line there exist two unit normal vectors defined via polarity with respect to $\langle\cdot\,,\cdot\rangle_{n,1}$.
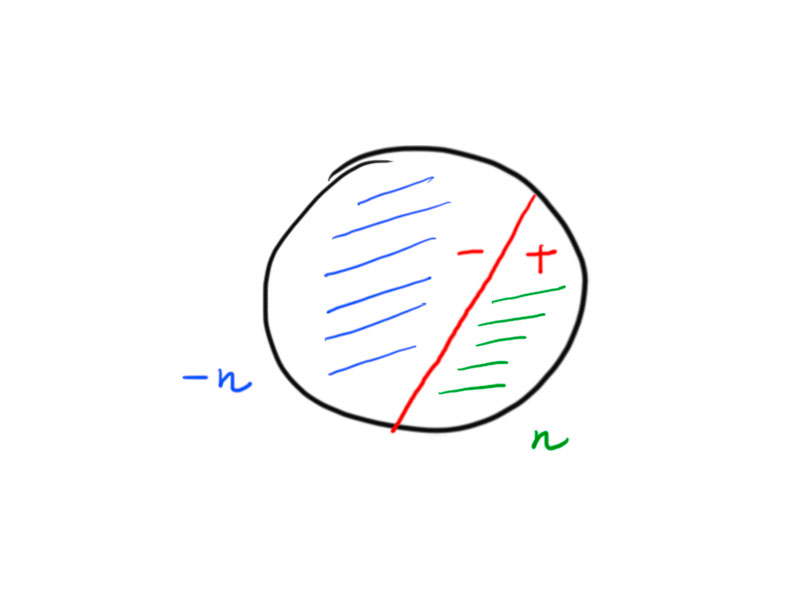
There is a bijection between half planes and vectors $n\in\R^{2,1}$ with $\langle n,n\rangle=1$.

Proposition
Let $\ell_1,\ell_2\in H^2$ be two distinct lines in the hyperbolic plane with unit normals $n_1$, $n_2$ (i.e. $\langle n_1,n_1\rangle=1$ and $\langle n_1,p\rangle=0$ for all $p\in\ell_1$).
Then the following are equivalent:

1. The two lines intersect.
2. $\operatorname{span}(n_1,n_2)$ has signature $(++)$.
3. $\lvert\langle n_1,n_2\rangle_{2,1}\rvert<1$.

Proof
(i)$\Rightarrow$(ii): Let $\ell_1\cap\ell_2=:x$.
Then $\operatorname{span}\{x\}$ has signature $(-)$, since $\langle x,x\rangle=-1$.
Thus $\operatorname{span}\{x\}^\perp$ has signature $(++)$ and $n_1,n_2\in\operatorname{span}\{x\}^\perp$.
This implies $\operatorname{span}\{n_1,n_2\}=\operatorname{span}\{x\}^\perp$ has signature $(++)$.

(ii)$\Rightarrow$(i) can be shown similarly.

(ii)$\Leftrightarrow$(iii):
The matrix for $\langle\cdot\,,\cdot\rangle\big\vert_{\operatorname{span}\{n_1,n_2\}}$ is given by
\[A=\begin{pmatrix}\langle n_1,n_1\rangle&\langle n_1,n_2\rangle\\\langle n_1,n_2\rangle&\langle n_2,n_2\rangle\end{pmatrix}=\begin{pmatrix}1&\langle n_1,n_2\rangle\\\&1\end{pmatrix}\,.\]
$A$ is positive definite if and only if $\operatorname{span}\{n_1,n_2\}$ is $(++)$, which is (ii).
But also, positive definiteness if equivalent to $1>0$ and $1-\langle n_1,n_2\rangle^2>0$, which is (iii).