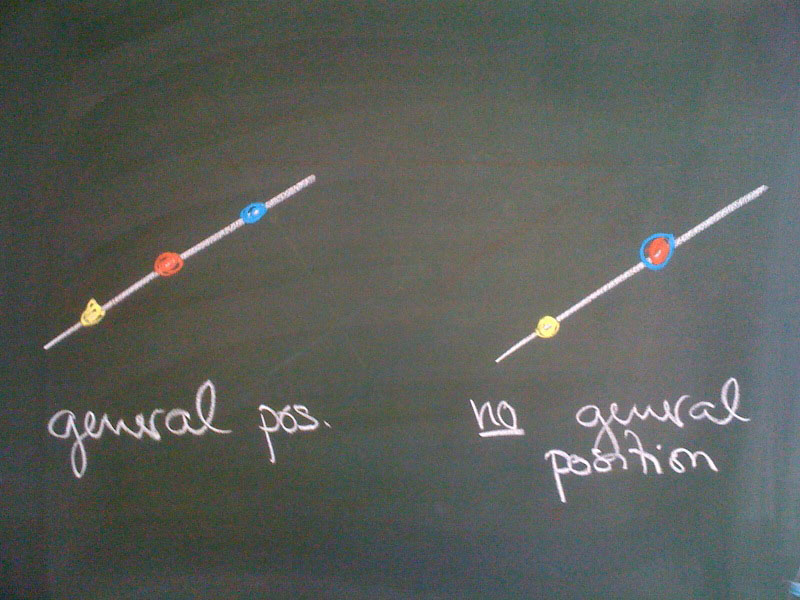
Definition. Let $P(V)$ be a projective space of dimension $n$. Then $n+2$ points in $P(V)$ are said to be in general position if no $n+1$ of them are contained in a $(n-1)$-dimensional projective subspace. In terms of linear algebra this implies that no $n+1$ representative vectors are linearly dependend, i.e. every $n+1$ are linearly independent.

Examples. If $n = 1$ we have to consider $n+2 = 3$ points on a projective line. These three points are in general position as long as they are disjoint.

Continue reading →

Projective Geometry

Let us start with a general definition for an arbitrary projective space. In this lecture we will almost entirely deal with real projective spaces.

Definition. Let $V$ be a vector space over an arbitrary field $F$. The projective space $P(V)$ is the set of $1$-dimensional vector subspaces of $V$. If $\dim(V) = n+1$, then the dimension of the projective space is $n$.

• A $1$-dimensional projective space is a projective line.
• A $2$-dimensional projective space is a projective plane.

Continue reading →