Definition. Let $P(V)$ be a projective space of dimension $n$. Then $n+2$ points in $P(V)$ are said to be in general position if no $n+1$ of them are contained in a $(n-1)$-dimensional projective subspace. In terms of linear algebra this implies that no $n+1$ representative vectors are linearly dependend, i.e. every $n+1$ are linearly independent.
Examples. If $n = 1$ we have to consider $n+2 = 3$ points on a projective line. These three points are in general position as long as they are disjoint.
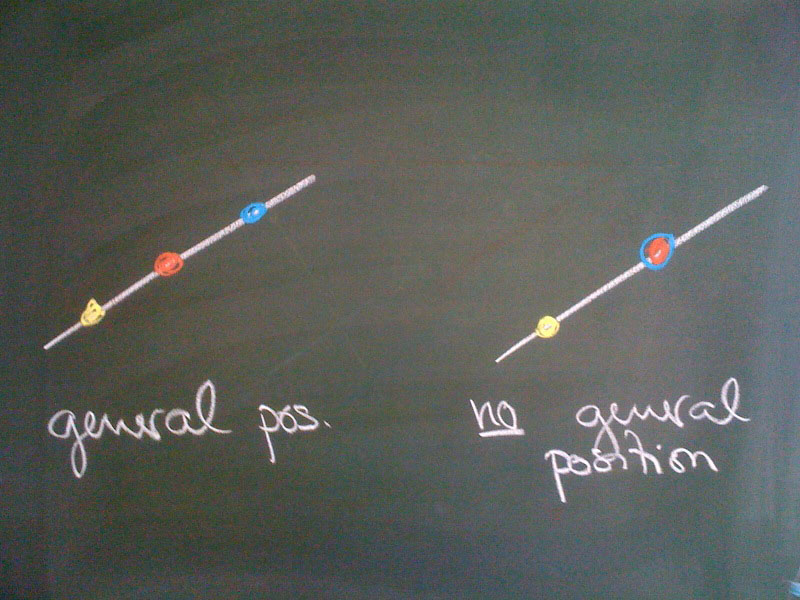
If $n = 2$ we have to consider $n+2 = 4$ points in a projective plane. The four points are in general position if no three are collinear.
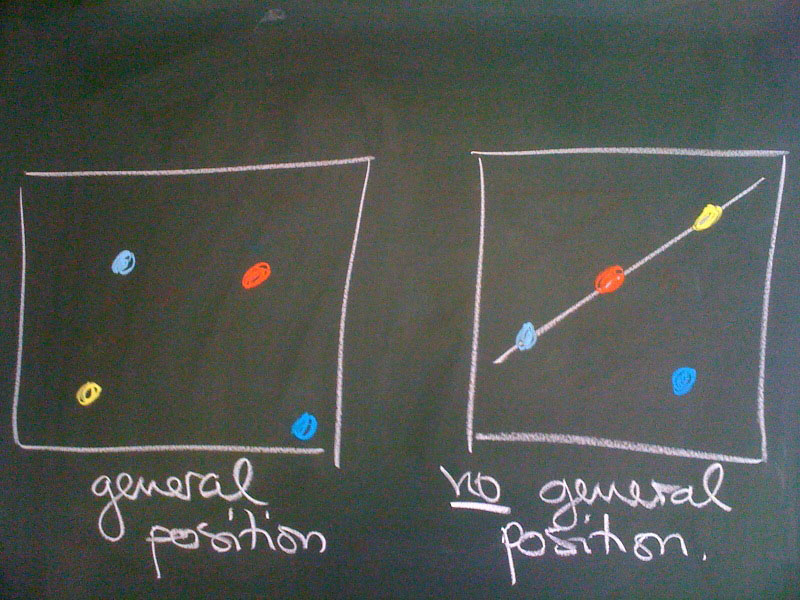
Question. The above pictures only show an affine part of the respective projective spaces. What happens if some of the points lie at infinity?
For points in general position there exists a canonical choice for the representative vectors described in the following lemma.
Lemma. Let $A_1, \ldots, A_{n+2}$ be $n+2$ points in general position in an $n$-dimensional projective space $P(V)$. Then there exist representative vectors $v_i \in V$ with $A_i = [v_i]$ for $i=1,\ldots,n+2$ such that:
\[
\sum_{i=1}^{n+2} v_i = 0.
\]
Moreover, this choice is unique up to a common scalar multiplicative factor, i.e., if $\tilde{v}_i = \mu_i v_i$ with $\mu_i \neq 0$ for $i=1,\ldots,n+2$ such that $\sum_{i=1}^{n+2} \tilde{v}_i = 0$ then $\mu_1 = \mu_2 = \ldots = \mu_{n+2}$.
Proof. Existence: Let $w_i$ with $A_i = [w_i]$ be representative vectors of the points $A_i$ for $i = 1,\ldots,n+2$. Since $\dim V = n+1$ the $n+2$ vectors are linearly dependent. So there exist $\lambda_i$ for $i = 1,\ldots,n+2$ not all equal to zero such that
\[
\sum_{i=1}^{n+2}\lambda_i w_i = 0.
\]
Since the points $A_i$ are in general position all $\lambda_i$ are non-zero. So setting $v_i = \lambda_i w_i$ we obtain $A_i = [v_i]$ with
\[
\sum_{i=1}^{n+2} v_i = 0.
\]
Uniqueness: Let $\tilde{v}_i = \mu_i v_i$ with $\mu_i \neq 0$ be a different set of representative vectors with
\[\sum_{i=1}^{n+2} \tilde{v}_i = 0.\]
From this equation we obtain the following system of $n+1$ homogeneous equations in $n+2$ variables:
\[
\sum_{i=1}^{n+2} \mu_i v_i = 0.
\]
Since the points $A_i$ are in general position the above system has rank $n+1$ and hence a $1$-dimensional set of solutions. But $(1,\ldots,1)$ is a solution of the system and hence there exists $\mu \neq 0$ with:
\[
(\mu_1, \ldots, \mu_{n+2}) = \mu (1,\ldots,1).
\]
So $\mu_1 = \ldots = \mu_{n+2} = \mu$.
Theorem [Pappus ~290-350 AC]. Let $A,B,C$ and $A’, B’, C’$ be two collinear triples of distinct points in the real projective plane. Then the points
\begin{eqnarray*}
A^{\prime\prime} &= (BC’) \cap (B’C) \\
B^{\prime\prime} &= (AC’) \cap (A’C) \\
C^{\prime\prime} &= (A’B) \cap (AB’)
\end{eqnarray*}
are collinear.
Proof. Without loss of generality let $A,B,B’$, and $C’$ be four points in general position. (Question: What happens if the points are not in general position?). Choose representative vectors $[a] = A$, $[b] = B$, $[b’] = B’$, and $[c’] = C’$ such that $a + b + b’ + c’ = 0$. Since $a,b,c’$ are linearly independent we obtain homogeneous coordinates:
\[
A = \sqvector{1\\ 0\\ 0}, \quad
B = \sqvector{0\\1\\ 0}, \quad
C’ = \sqvector{0\\ 0\\1}, \quad
B’ = \sqvector{-1\\-1\\-1}.
\]
Then
\begin{align*}
C =&\sqvector{1\\y\\ 0} \text{with $y \neq 0$ since $C \neq A$, and} \\
A’ =&\sqvector{1\\1\\z} \text{with $z \neq 1$ since $A’ \neq B’$.}
\end{align*}
The lines spanned by the six points are the following:
\begin{align*}
AB’ &= \left\{\left. \sqvector{x_1\\x_2\\x_3} \,\right\vert\, x_2 = x_3 \right\}\,, \\
A’B &= \left\{\left. \sqvector{x_1\\x_2\\x_3} \,\right\vert\, s \sqvector{1\\1\\z} + t\sqvector{0\\1\\ 0} = \sqvector{s\\s+t\\sz} \right\}\,, \\
AC’ &= \left\{\left. \sqvector{x_1\\x_2\\x_3} \,\right\vert\, x_2 = 0\right\}\,, \\
A’C &= \left\{\left. \sqvector{x_1\\x_2\\x_3} \,\right\vert\, s \sqvector{1\\1\\z} + t\sqvector{1\\y\\ 0} = \sqvector{s+t\\s+ty\\sz} \right\}\,, \\
BC’ &= \left\{\left. \sqvector{x_1\\x_2\\x_3} \,\right\vert\, x_1 = 0\right\}\,, \\
B’C &= \left\{\left. \sqvector{x_1\\x_2\\x_3} \,\right\vert\, s\sqvector{-1\\-1\\-1} + t\sqvector{1\\y\\ 0} = \sqvector{-s+t\\-s+ty\\-s} \right\}\,.
\end{align*}
For the points of intersection $A^{\prime\prime}$, $B^{\prime\prime}$, and $C^{\prime\prime}$ this implies:
\begin{align*}
C^{\prime\prime} &= AB’ \cap A’B = \sqvector{1\\z\\z}\,, \\
B^{\prime\prime} &= AC’ \cap A’C = \sqvector{1-y\\ 0\\-yz}\,, \\
A^{\prime\prime} &= BC’ \cap B’C = \sqvector{0\\y-1\\-1}\,.
\end{align*}
Now we construct a linear dependence to show that the three points are collinear:
\[
z \sqvector{0\\y-1\\-1} – \sqvector{1-y\\ 0\\-yz} + (1-y) \sqvector{1\\z\\z} =
\sqvector{y-1+1-y \\ z(y-1) + (1-y)z \\ -z + yz + (1-y)z} = 0\,.
\]
So $A^{\prime\prime}$, $B^{\prime\prime}$, and $C^{\prime\prime}$ are collinear.
Remarks.
- The Pappus configuration is very symmetric in the following respect: It consists of nine lines and nine points and each line contains three points and each point lies on three lines.
- Hilbert showed in 1899 that Pappus Theorem “corresponds” to the commutativity of multiplication. That is, a synthetic geometry that satisfies Pappus Theorem corresponds to the geometry of a projective space that is the projectivation of a vectorspace over a field.

In the proof of Pappus’ theorem, why can we choose A, B, B’ and C explicitly?
Let $A = P(U_A), B = P(U_B), B^\prime =P(U_{B^\prime}), C^\prime = P(U_{C^\prime})$. Since they are in general position you can find $a \in U_A, b \in U_B, c^\prime \in U_{C^\prime}$ s.t. they are linearly independent. Now take $b^\prime \in U_{B^\prime} \setminus \{0\}$. Analogously to one Lemma we had, there are $\lambda_1, \dots, \lambda_3$ with $\lambda_1a + \lambda_2 b + \lambda_3 c^\prime = -b^\prime$. It holds $\lambda_i \ne 0$ for every $i$ because the points are in general position. Therefore $(\lambda_1a , \lambda_2 b , \lambda_3 c^\prime)$ is a basis of $V$ and we get $A = [e_1], B = [e_2], C^\prime = [e_3], B^\prime = [-e_1-e_2-e_3]$ as homogeneous coordinates, which depend on the chosen basis of $V$ (see def.).
Hopefully this is right and answers your question.
Thank you for clarification. In both of your comments it should be $C^\prime$ instead of $C$. ($A$, $B$, and $C$ are collinear.) But the rest is perfect.
You always have to bare in mind, that coordinates are with respect to a chosen basis – as xoto pointed out correctly. Sometimes people add the basis to the coordinates to make this explicit: If $\mathcal{B} = \{a,b,c\}$ is a basis, then $a = \svector{1\\0\\0}_\mathcal{B}$, $b = \svector{0\\1\\0}_\mathcal{B}$, and $c = \svector{0\\0\\1}_\mathcal{B}$.