Author Archives: Thilo Rörig

Lecture 3

Posted on by
3

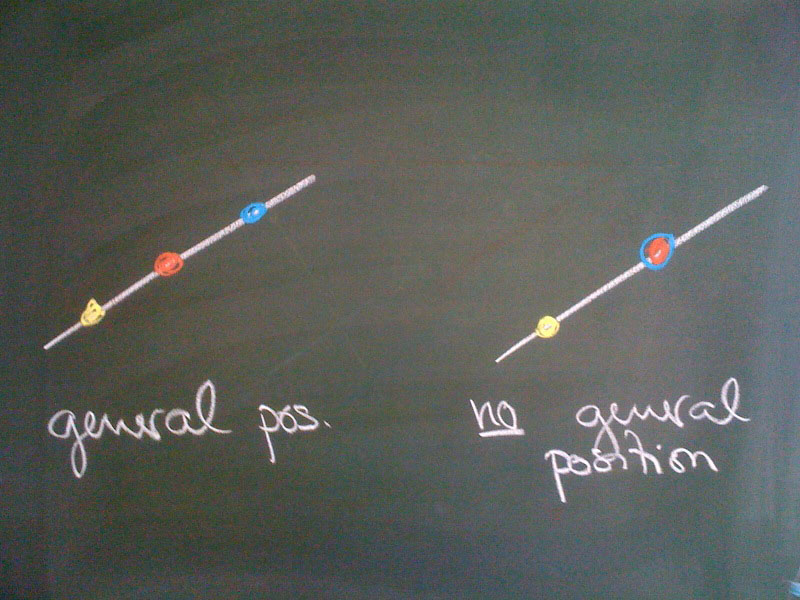
Definition. Let $P(V)$ be a projective space of dimension $n$. Then $n+2$ points in $P(V)$ are said to be in general position if no $n+1$ of them are contained in a $(n-1)$-dimensional projective subspace. In terms of linear algebra this implies that no $n+1$ representative vectors are linearly dependend, i.e. every $n+1$ are linearly independent.

Examples. If $n = 1$ we have to consider $n+2 = 3$ points on a projective line. These three points are in general position as long as they are disjoint.
Points in general position on a projective line

Continue reading →

Lecture 2

Posted on by
Reply

Projective Geometry

Let us start with a general definition for an arbitrary projective space. In this lecture we will almost entirely deal with real projective spaces.

Definition. Let $V$ be a vector space over an arbitrary field $F$. The projective space $P(V)$ is the set of $1$-dimensional vector subspaces of $V$. If $\dim(V) = n+1$, then the dimension of the projective space is $n$.

  • A $1$-dimensional projective space is a projective line.
  • A $2$-dimensional projective space is a projective plane.

Continue reading →

Lecture 1

Posted on by
Reply

Historical Remarks

The word geometry is of Greek origin ($\gamma\varepsilon\omega\mu\varepsilon\tau\rho\iota\alpha$) and means “measurement of the earth”. But the first accounts were found in Egypt and Mesopotamia (today Iraq) around 2000 BC. It was known how to calculate simple areas and volumes and people of that time already had an approximation of $\pi$. But no general statements/theorems and proofs were found. Around 600 BC in Greece, Thales was the first to deduce theorems from a set of axioms. At about 300 BC, Euclid wrote the book Elements in which he states the five axioms of what is today called Euclidean geometry. His fifth axioms is known as the parallel postulate and can be phrased as follows:

Given a line and a point not on this line, there is a unique line through the point parallel to the line.

Continue reading →

Welcome to Geometry I

Posted on by
2

This site keeps track of the content of the Geometry I Course taught at the Technical University Berlin during winter term 2012/13. It is the first time that I try to create lively lecture notes this way and I hope that the students and myself will create great notes, discuss the content, and enjoy the final result.

The first thing you need to do is to register. Then you will be able to contribute your own thoughts and to comment on other peoples post. To register, please write an email to Emanuel (huhnen[at]math.tu-berlin.de) that contains your desired username (minimum 4 characters, only lower case letters and numbers) and the email address you want to use for the blog. We will then create your account and you will receive an invitation email to join the blog.

Enjoy.