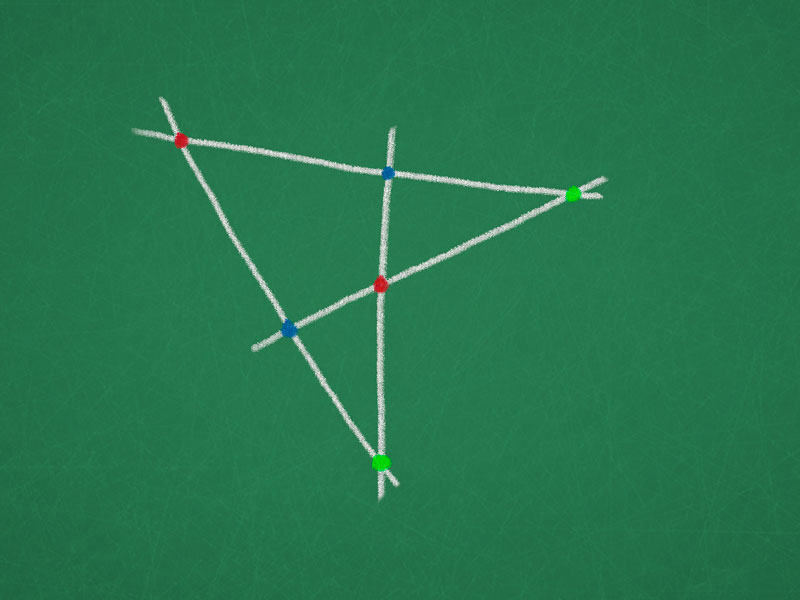
Complete quadrilateral and quadrangle

Definition (complete quadrilateral). A configuration consisting of four lines in the projective plane – no three through one point – and the six intersection points, one for each pair of lines, form a complete quadrilateral.

Continue reading →

Cross-ratio (Doppelverhältnis)

We are looking for invariants with respect to projective transformations.

Definition: Let $ P_{i} =[v_i]= \ssqvector{x_{i} \\ y_{i}}$, $i=1,\ldots,4$, be four distinct points on a projective line $ \RP^{1} $. Then the cross-ratio of these points is

\begin{align*}
cr(P_{1},P_{2},P_{3},P_{4})
&= \frac{\det(v_1v_2)}{\det(v_2v_3)}\frac{\det(v_3v_4)}{\det(v_4v_1)}\\
&= \dfrac{x_{1}y_{2}-x_{2}y_{1}}{x_{2}y_{3}-x_{3}y_{2}} \dfrac{x_{3}y_{4}-x_{4}y_{3}}{x_{4}y_{1}-x_{1}y_{4}}.\\
\end{align*}

If $y_{i} \neq 0$, we may introduce affine coordinates $ u_{i} = \frac{x_{i}}{y_{i}}$. This yields

\begin{align*}
cr(P_{1},P_{2},P_{3},P_{4}) =
&= \dfrac{y_{1}y_{2}( \frac{x_{1}}{y_{1}}-\frac{x_{2}}{y_{2}} ) }{y_{2}y_{3}( \frac{x_{2}}{y_{2}}-\frac{x_{3}}{y_{3}} )} \dfrac{y_{3}y_{4}( \frac{x_{3}}{y_{3}}-\frac{x_{4}}{y_{4}} ) }{y_{4}y_{1}( \frac{x_{4}}{y_{4}}-\frac{x_{1}}{y_{1}} )} \\
&= \dfrac{u_{1}-u_{2}}{u_{2}-u_{3}} \dfrac{u_{3}-u_{4}}{u_{4}-u_{1}}\,.
\end{align*}

Continue reading →

Projective transformations

Let $V$, $W$ be two vectorspaces over the same field and of the same dimension and $F\colon V \rightarrow W$ a linear isomorphism. In particular $ker(F) = \{0\}$, so F maps 1-dimensional subspaces to 1-dimensional subspaces.

Hence $F$ induces a map from $P(V)$ to $P(W)$.

Definition: A projective transformation $f$ from $P(V)$ to $P(W)$ is a map defined by a linear isomorphism $F\colon V \rightarrow W$ such that

\begin{equation*}
f([v]) = [F(v)] \quad \forall [v] \in P(V)\,.
\end{equation*} Continue reading →