Complete quadrilateral and quadrangle
Definition (complete quadrilateral). A configuration consisting of four lines in the projective plane – no three through one point – and the six intersection points, one for each pair of lines, form a complete quadrilateral.
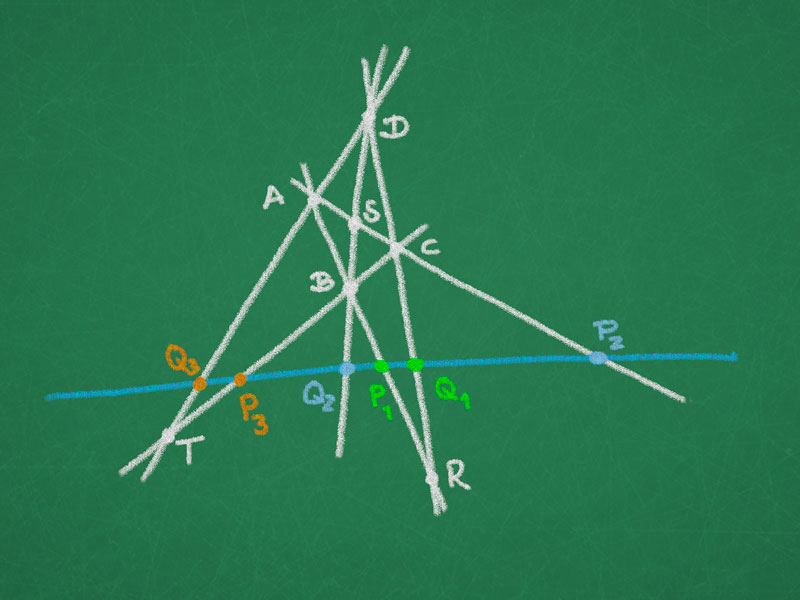
Definition (complete quadrangle). Let $A$, $B$, $C$ and $D$ be four points in general position in a projective plane. The complete quadrilateral consists of these four points and six lines – one for each pair of points. The lines spanned by disjoint sets of points are called opposite.
Definition (quadrangular set). Let $\ell$ be a line not through any of the points $A$, $B$, $C$ and $D$. We obtain three pairs of intersection points $P_i$, $Q_i$ for $i=1,2,3$ with the three pairs of opposite lines. The set $\{ P_1, Q_1; P_2,Q_2; P_3,Q_3\}$ is called a quadrangular set.
Note the symmetry of the configuration with respect to the exchange of $P_i$ and $Q_i$ and the permutation of the indices $1$, $2$, $3$.
Definition (multi-ratio). Let $P_1, P_2, \ldots, P_6$ be six points on a projective line with representative vectors $P_i = [v_i]$ for $i=1, \ldots, 6$. The multi-ratio of these six points is:
\[
\mathrm{m}(P_1,P_2,P_3,P_4,P_5,P_6) =
\frac{\det(v_1 v_2)}{\det(v_2 v_3)}
\frac{\det(v_3 v_4)}{\det(v_4 v_5)}
\frac{\det(v_5 v_6)}{\det(v_6 v_1)} .
\]
Properties of the multi-ratio:
- The multi-ratio is well-defined and independent of the choice of homogeneous coordinates.
- The multi-ratio is a projective invariant.
- For the calculation we may use affine coordinates and if one of the coordinates is infinite, we may cancel them as we did in the calculation of the cross-ratio.
- The multi-ratio can be calculated via cross-ratios: \[ \mathrm{m}(P_1,P_2,P_3,P_4,P_5,P_6) = (-1) \cr(P_1,P_2,P_3,P_4) \cr(P_1,P_4,P_5,P_6).\]
Theorem. A quadrangular set of points is characterized by the relation
\[
\mathrm{m}(P_1,Q_2,P_3,Q_1,P_2,Q_3) = -1.
\]
Any five points of a quadrangular set determine the sixth point.
Proof. We will use the relation between croos-ratio and multi-ratio to prove the relation. So
\[
\mathrm{m}(P_1,Q_2,P_3,Q_1,P_2,Q_3)
= (-1) \cr(P_1,Q_2,P_3,Q_1) \cr(P_1,Q_1,P_2,Q_3).
\]
The central projection of the line $CD$ to the line $\ell$ from $A$ and $D$ yields the following two equations:
\begin{align*}
CD\xrightarrow A\ell\colon\cr(D,C,Q_1,R) &= \cr(P_1,Q_3,P_2,Q_1) = \frac{1}{\cr(P_1,Q_1,P_2,Q_3)} \\
CD\xrightarrow B\ell\colon\cr(R,D,C,Q_1) &= \cr(P_1,Q_2,P_3,Q_1)
\end{align*}
Thus we obtain for the multiratio:
\begin{align*}
\mathrm{m}(P_1,Q_2,P_3,Q_1,P_2,Q_3)
&= (-1) \cr(P_1,Q_2,P_3,Q_1) \cr(P_1,Q_1,P_2,Q_3) \\
&= – \cr(D,C,Q_1,R) \frac{1}{\cr(D,C,Q_1,R)} = -1.
\end{align*}
If five points are given we can easily see for example using affine coordinates that the relation $\mathrm{m}(P_1,Q_2,P_3,Q_1,P_2,Q_3) = -1$ determines the affine coordinate of the sixth point, and hence the point itself.
Pappus Theorem on quadrangular sets. Let $\{P_1,Q_1; P_2,Q_2; P_3,Q_3\}$ be a quadrangular set of points on a projective line. Let $A$, $B$, and $C$ be three distinct points such that $ABP_1$, $ACP_2$, and $BCP_3$ are collinear. Then the lines $Q_1C$, $Q_2B$, and $Q_3A$ intersect in one point.
In other words, we may construct a complete quadrilateral for a quadrangular set.
Proof. Let $D = Q_1C \cap Q_2B$ and $\tilde Q_3 = AD \cap \ell$. Then both $\{P_1,Q_1; P_2,Q_2; P_3,Q_3\}$ and $\{P_1,Q_1; P_2,Q_2; P_3,\tilde{Q}_3\}$ are quadrangular sets. But since five of the points coincide we have $\tilde Q_3 = Q_3$ and hence the points $A$, $D$, and $Q_3$ lie on one line.
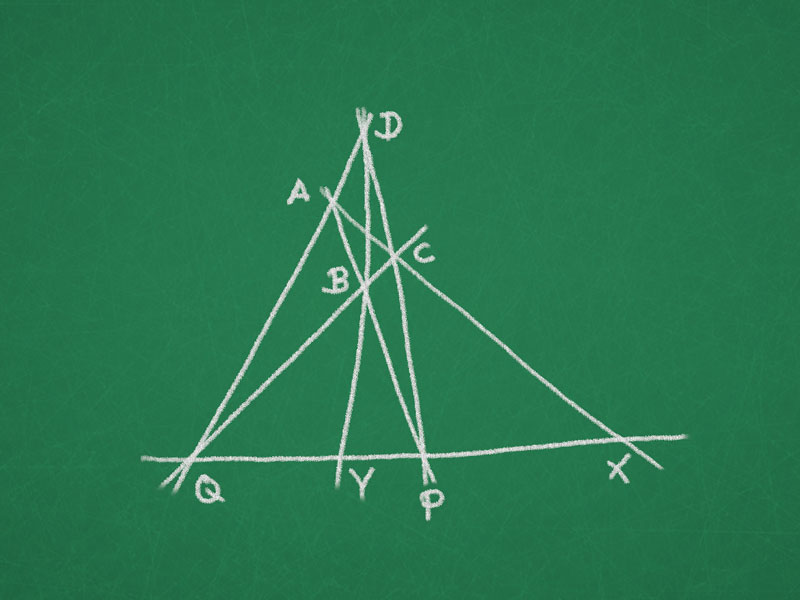
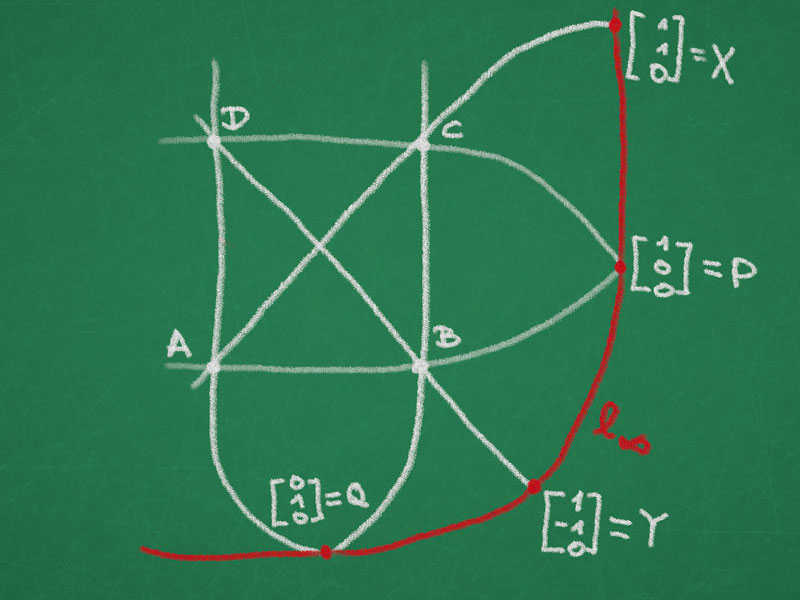
Theorem (complete quadrilateral). Let $\ell_1$, $\ell_2$, $\ell_3$, and $\ell_4$ be four lines in the projective plane such that no three go through one point. Further let $A = \ell_1 \cap \ell_2$, $B = \ell_2 \cap \ell_3$, $C = \ell_3 \cap \ell_4$, $D = \ell_4 \cap \ell_1$, and $P = \ell_1 \cap \ell_3$ and $Q = \ell_2 \cap \ell_4$ be the six points of the complete quadrilateral. Define $\ell = PQ$ and $X = AC \cap \ell$ and $Y = BD \cap \ell$. Then
\[
\cr(P,X,Q,Y) = -1.
\]
Remark. We say that the pair $\{P,Q\}$ seperates the pair $\{X,Y\}$ harmonically or $Y$ is the harmonic conjugate of $X$ with respect to $\{P,Q\}$ if $\cr(P,X,Q,Y) = -1$.
Computational proof. We can apply a projective transformation of the plane to map the four points $A$, $B$, $C$, and $D$ onto the unit square with vertices
\[
\sqvector{0\\ 0\\1}, \quad
\sqvector{1\\ 0\\1}, \quad
\sqvector{1\\1\\1}, \quad
\sqvector{0\\1\\1}.
\]
Then the line $\ell$ is the line at infinity and we can easily calculate the cross-ratio and see it is equal to $-1$.