Note If a conic in $\mathbb{R}P^{2}$ contains a line, then it is degenerate.

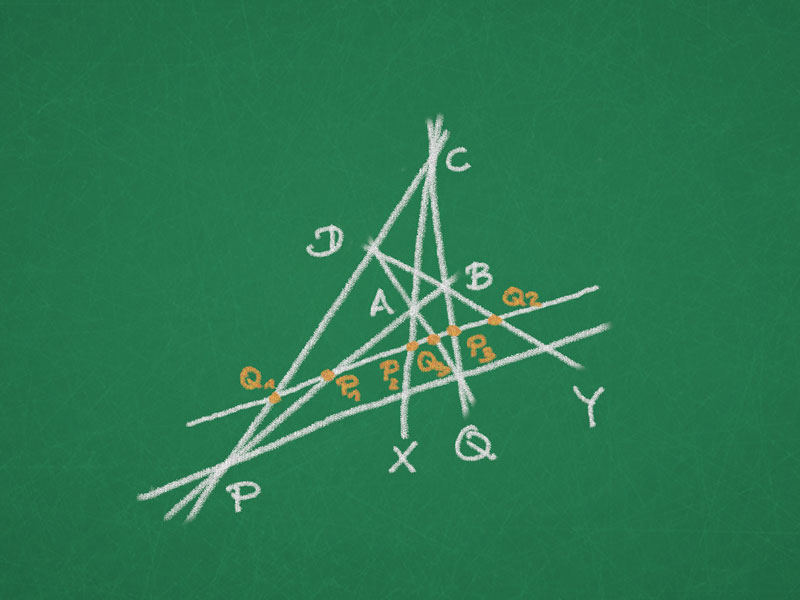
Theorem. Through five points $P_{1},P_{2},P_{3},P_{4},P_{5} \in \mathbb{R}P^{2}$ there exists a conic in $\mathbb{R}P^{2}$.

$i)$ If no four points lie on a line, then the conic is unique.

$ii)$ If no three lie on one line (five points in general position), then the conic is non-degenerate.

Lemma. If a conic contains three collinear points, then it contains the line through these points. Continue reading →

Definition.
Let $V$ be a vector space over $\mathbb{R}$ (or $\mathbb{C}$). A map
$b\colon V \times V \to \mathbb{R}$ is a symmetric bilinear form, if

1. $ b(v,w)=b(w,v) \quad \forall v,w \in V $
2. $ b(\alpha_1 v_1 + \alpha_2 v_2,w) = \alpha_1 b(v_1,w) +
   \alpha_2 b(v_2,w)$ for all $\alpha_1,\alpha_2 \in \mathbb{R}$, $v_1, v_2, w \in V$.

$b$ is non-degenerate, if
\[b(v,w)=0 \quad \forall w \in V \Rightarrow v=0\,.\]
The corresponding quadratic form is defined by
\[q(v)=b(v,v) \quad \forall v \in V\,.\]

Continue reading →

Cross-ratio of lines through a point (again).

Claim. The map which maps a point $g^{\ast} \in p^{\ast}$ to the intersection point of $g \cap \ell$ is a projective map. Continue reading →

Let $\ell$ be a line in $\RP^2$. Then the line can be described by one homogeneous equation:
$$\begin{bmatrix}
x_1\\
x_2\\
x_3\end{bmatrix}\in l \Longleftrightarrow a_1x_1+a_2x_2+a_3x_3=0\,,$$
where the $a_i$ are unique up to a scalar multiple $\lambda\neq0$. We can take in a way that will be explained in detail, the point $[a_1,a_2,a_3]^T$ as homogeneous coordinates for the line $\ell$. The lines in $\RP^2$ yield another projective plane with homogeneous coordinates $[a_1,a_2,a_3]^T$. This is what we call the dual projective plane $(\RP^2)^*$. If we fix one point $[x_1,x_2,x_3]^T\in \RP^2$, the set of lines through this point corresponds to a line in $(\RP^2)^*$.

Continue reading →

Fundamental Theorem of real projective geometry: Let $f\colon \RP^n \to \RP^n$, $n \ge 2$, be a bijective map that maps lines to lines. Then $f$ is a projective transformation.

Remark: The theorem does not hold for arbitrary fields. For example $f\colon \CP^n \to \CP^n$ ($n \ge 2$) with
\[f\left(\sqvector{z_1\\ \vdots\\ z_{n+1}}\right) = \sqvector{\bar z_1\\ \vdots\\ \bar z_{n+1}}\]
is a bijective map, mapping complex projective lines to complex projective lines but it is not a projective transformation of $\CP^n$.

Continue reading →

Theorem (complete quadrilateral). Consider four lines with intersection points $A$, $B$, $C$, $D$, $P$, and $Q$ as shown in the picture. Then the cross-ratio of the intersection points $X$ and $Y$ of the diagonals with the line $PQ$ and $P$ and $Q$ is:

\[ \cr(P,X,Q,Y)=−1.\]

Proof of theorem on complete quadrilateral (multi-ratio).
Consider the multi-ratio with

$P_{1} = Q_{1} = P$, $P_{3} = Q_{3} = Q$, $Q_{2} = X$, $P_{2} = Y$,

where $p$ is the affine coordinates of $P$, $q$ the ones of $Q$ etc.

\begin{align}
-1 &= \mathrm{m}(P, X, Q, P, Y, Q) \\
&= \frac{p-x}{x-q} \frac{q-p}{p-y} \frac{y-q}{q-p} \\
&= \frac{p-x}{x-q} \frac{q-y}{y-p} \\
&= \mathrm{cr}(P, X, Q, Y). \\
\end{align}

$\square$

Continue reading →