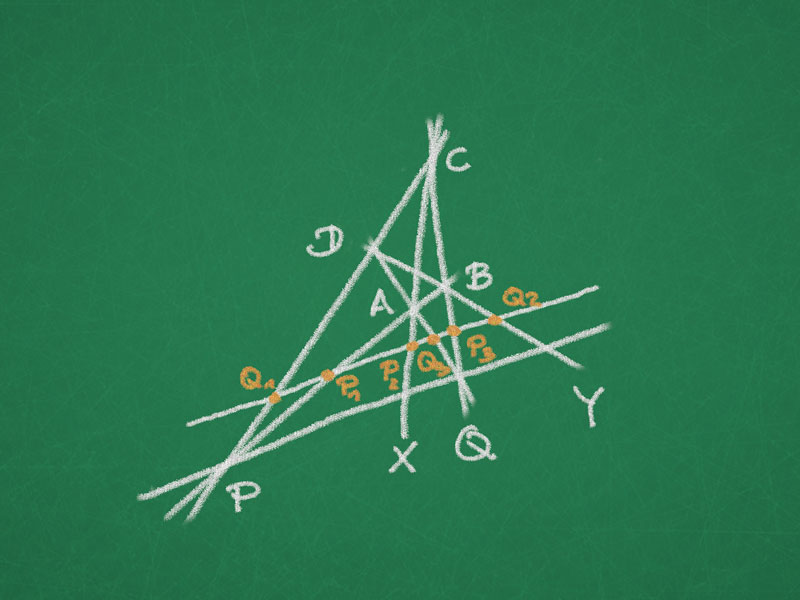
Theorem (complete quadrilateral). Consider four lines with intersection points $A$, $B$, $C$, $D$, $P$, and $Q$ as shown in the picture. Then the cross-ratio of the intersection points $X$ and $Y$ of the diagonals with the line $PQ$ and $P$ and $Q$ is:

\[ \cr(P,X,Q,Y)=−1.\]

 

Proof of theorem on complete quadrilateral (multi-ratio).
Consider the multi-ratio with

$P_{1} = Q_{1} = P$, $P_{3} = Q_{3} = Q$, $Q_{2} = X$, $P_{2} = Y$,

where $p$ is the affine coordinates of $P$, $q$ the ones of $Q$ etc.

\begin{align}
-1 &= \mathrm{m}(P, X, Q, P, Y, Q) \\
&= \frac{p-x}{x-q} \frac{q-p}{p-y} \frac{y-q}{q-p} \\
&= \frac{p-x}{x-q} \frac{q-y}{y-p} \\
&= \mathrm{cr}(P, X, Q, Y). \\
\end{align}

$\square$

Projective involutions

Consider a projective map $f\colon \RP^1 \to \RP^1$.
$f$ is a projective involution if $f \not= id$ but $f^2 = id$.

$f$ can be defined by two pairs of points $A$,$B$ and $C$,$D$ such that:

\begin{align}
f(A) &= B, &f(B) = A \\
f(C) &= D, &f(D) = C \\
\end{align}

$f$ has either $0$ or $2$ fixed points. (homework)

If $f$ is a projective involution with two fixed points $P, Q$, then

\begin{align}
\mathrm{cr}(P, X, Q, f(X)) &= \mathrm{cr}(P, f(X), Q, X) \\
&= \frac{1}{\mathrm{cr}(P, X, Q, f(X))} \\
\end{align}

$\Rightarrow \mathrm{cr}(P, X, Q, f(X)) = \pm 1 \quad \forall X \not= P, Q$

Since $\mathrm{cr} \not= 1$ we obtain a characteristic equation for a projective involution with two fixed points:

$\mathrm{cr}(P, X, Q, f(X)) = -1 \quad \forall X \not= P, Q$.

Proof of theorem on complete quadrilateral (projective involution)
Consider $f\colon \RP^1 \rightarrow \RP^1$ with

$A \xrightarrow f B$
$B \rightarrow A$
$C \rightarrow D$
$D \rightarrow C$.

This map is a projective involution. So $f|_\ell$ is also an involution with fixed points $P$ and $Q$. Further $f(X) = Y$.
$\Rightarrow \mathrm{cr}(P, X, Q, Y) = -1$.

$\square$

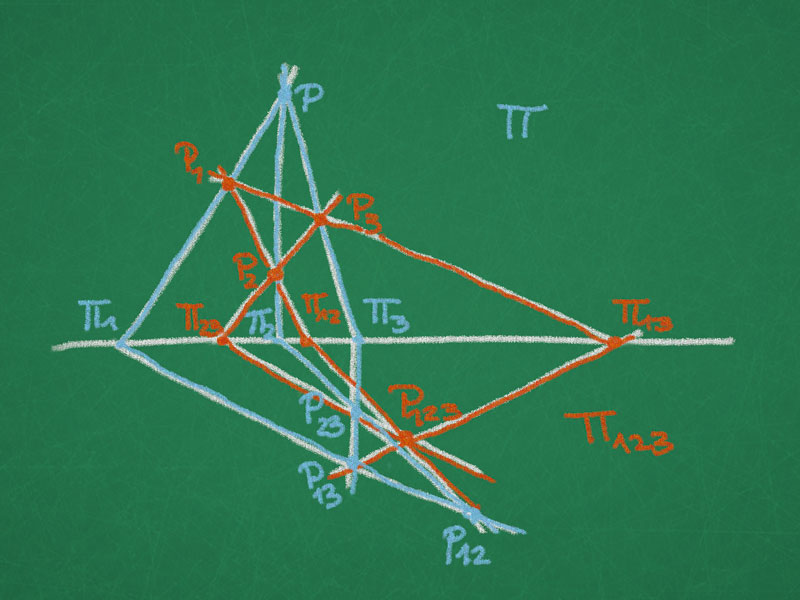
Möbius pair of tetrahedra

Definition (Moebius-pair): A pair of tetrahedra is called a Moebius-pair if the vertices of one tetrahedra lie in the planes spanned by the faces of the second and the vertices of the second lie in the face-planes of the first.

Theorem. If four vertices of the first tetrahedron lie in the four face-planes of the second and three of the vertices of the second tetrahedron lie in the three face-planes of the first then the fourth vertex lies in the fourth plane.

( $\rightsquigarrow$ Geometry II, consistency of nets. Bobenko, Suris: Discrete Differential Geometry)

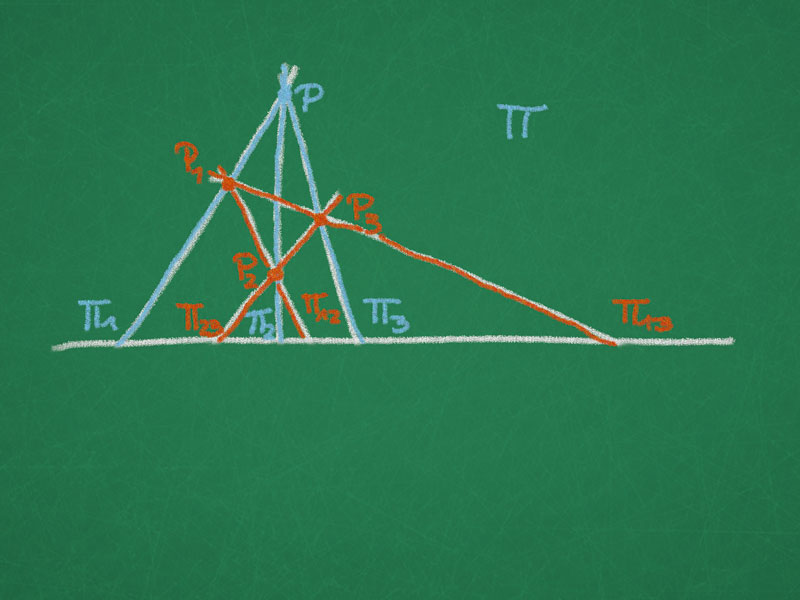
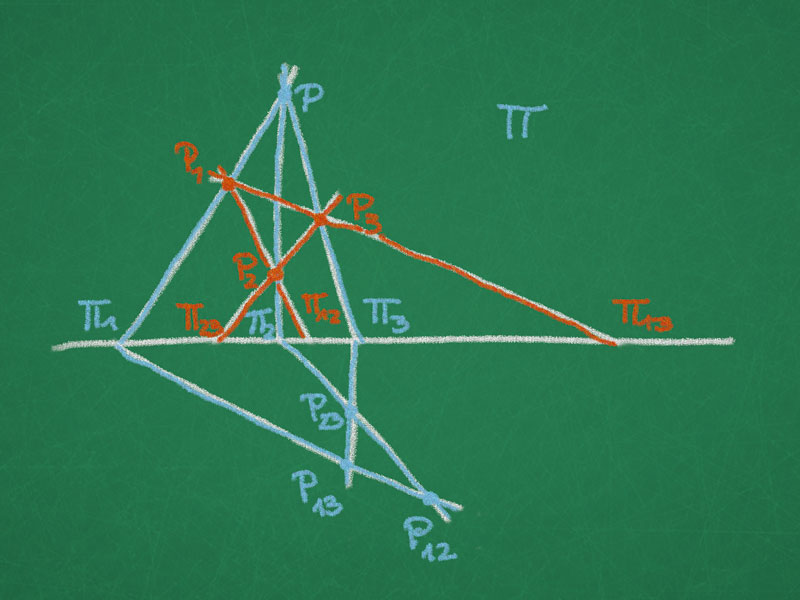
Proof. Let us introduce the following labelling motivated by a (combinatorial) cube:

The vertices of two tetrahedra $T_1$ and $T_2$ are:

$ \quad$ $T_1$ $: P, P_{12}, P_{13}, P_{23}$
$ \quad$ $T_2$ $: P_1, P_2, P_3, P_{123}$

The face-planes are labelled:

\begin{align}
T_1 : \Pi_1 &\ni P, P_{12}, P_{13} &T_2 : \Pi_{12} &\ni P_1, P_2, P_{123}\\
\Pi_2 &\ni P, P_{12}, P_{13} &\Pi_{13} &\ni P_1, P_3, P_{123}\\
\Pi_3 &\ni P, P_{13}, P_{23} &\Pi_{23} &\ni P_2, P_3, P_{123}\\
\Pi_{123} &\ni P_{12}, P_{23}, P_{13} &\Pi &\ni P_1, P_2, P_3
\end{align}

Now seven vertices lie on seven planes:

$P_i$ $\in$ $\Pi_i$, $P$ $\in$ $\Pi$, $P_{ij}$ $\in$ $\Pi_{ij}$

Show: $P_{123}$ $\in$ $\Pi_{123}$.

The plane $\Pi$ contains the vertices $P$, $P_1$, $P_2$, and $P_3$. The intersections of the planes $\Pi_i$ and $\Pi_{ij}$ with $\Pi$ form a complete quadrangle. This yields a quadrangular set on the line $\Pi \cap \Pi_{123}$.

Now we have a look at the intersection of the planes $\Pi_i$ and $\Pi_{ij}$ with $\Pi_{123}$. The lines $\Pi_{i} \cap \Pi_{123}$ yield a triangle on the vertices $P_{12}$, $\Pi_{13}$, and $\Pi_{23}$.

By the Theorem of Pappus on quadrangular sets of Lecture 7 the lines $\Pi_{ij} \cap\Pi_{123}$ through the points $\Pi_{ij}$ intersect in one point on $\Pi_{123}$. This point is $P_{123}$ and it lies on $\Pi_{123}$.

$\square$

Koenigs-cube

Definition (Koenigs-cube). A Koenigs-cube is a combinatorial cube with six flat faces (i.e. $P, P_i, P_j, P_{ij}$ and $P_i, P_{ij}, P_{ik}, P_{123}$ lie in a plane) such that the vertices $P, P_{12}, P_{13}, P_{23}$ and $P_1, P_2, P_3, P_{123}$ each lie in a plane.

Theorem. If the red vertices ($P, P_{12}, P_{13}, P_{23}$) lie in a plane and all the faces are flat, then the blue vertices ($P_1, P_2, P_3, P_{123}$) lie in a plane.

Proof. homework.