Due Friday, January 10.
This assignment is about the discretization of the Laplacian using FEM on triangular meshes, and the harmonic forms of the Hodge decomposition. Feel free to ask any questions by writing a blog post!
1. ( The stiffness matrix — 10 pts. ) On a discrete triangular mesh \(M\), the stiffness matrix \(L\) is given by
\begin{align*}
L_{ij} = -\int_M d \varphi_{i}\wedge *d\varphi_j = -\sum_{t_{ijk}\succ e_{ij}}\langle\textrm{grad}\varphi_i,\textrm{grad}\varphi_j\rangle A_{ijk}
\end{align*}
where \(A_{ijk}\) is the area of triangle \(t_{ijk}\). Here we used the fact that the hat functions \(\varphi_i\), \(\varphi_j\) are piecewise linear and hence their gradients are piecewise constant on the triangles. We also used the fact that \(\textrm{grad}\varphi_i\) and \(\textrm{grad}\varphi_j\) have common support (the region on which the function is non-zero) only on the triangles incident to both \(i\) and \(j\).
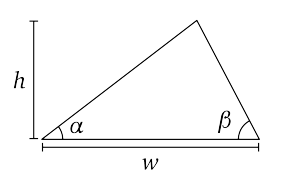
(a) Show that the aspect ratio of a triangle can be expressed as the sum of the cotangents of the interior angles at its base, i.e.,
\begin{align*}
\frac{w}{h} = \cot\alpha + \cot\beta.
\end{align*}
(b) Show that the gradient of the hat function on triangle \(t_{ijk}\) is given by
\begin{align*}
\textrm{grad}\varphi_i = \frac{e_{jk}^{\bot}}{2A_{ijk}}
\end{align*}
where \(e^{\bot}_{jk}\) is the vector \(e_{jk}\) rotated \(90^\circ\) counterclockwise within \(t_{ijk}\).
(c) Show that for any hat function \(\varphi_i\) associated with vertex \(p_i\) of triangle \(t_{ijk}\), \[\langle\textrm{grad}\varphi_i,\textrm{grad}\varphi_i\rangle A_{ijk}=\tfrac{1}{2}(\cot\alpha+\cot\beta).\]
(d) Show that for the hat functions \(\varphi_i\) and \(\varphi_j\) associated with vertices \(p_i\) and \(p_j\) of triangle \(t_{ijk}\), we have
\begin{align*}
\langle\textrm{grad}\varphi_i,\textrm{grad}\varphi_j\rangle A_{ijk} = -\tfrac{1}{2}\cot\theta
\end{align*}
where \(\theta\) is the angle between the opposite edge vectors.

Putting all these facts together, we have the infamous cotan formula
\begin{align*}
(Lu)_i = \tfrac{1}{2}\sum_{e_{ij}\succ p_i}(\cot\alpha_{ij}+\cot\beta_{ij})(u_j-u_i).
\end{align*}
where \(\alpha_{ij}\) and \(\beta_{ij}\) are the angles of opposite vertices across from \(e_{ij}\) in the two adjacent triangles.
2. ( Harmonic forms on closed manifolds — 10 pts. ) Show that, on a closed manifold \(M\) without boundary,
\begin{align*}
{\cal H}^k(M) = \left\{h\in\Omega^kM~\Big|~\Delta h = 0\right\},\quad\mbox{where \(\Delta = -d\delta – \delta d\).}
\end{align*}
That is, harmonic fields are the solutions to the Laplace’s equation, and vice versa. What happens if \(M\) has a boundary?
