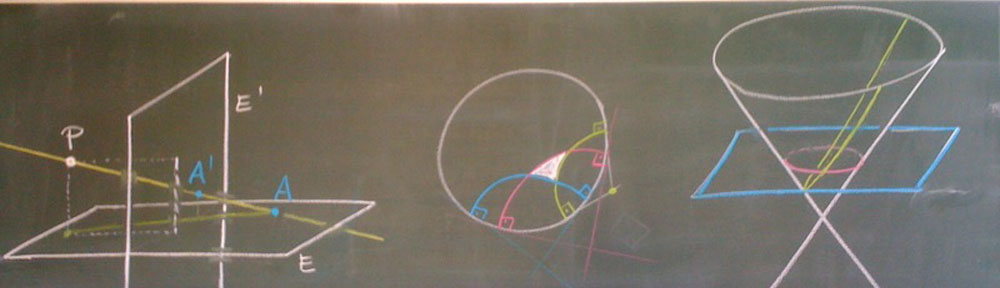Definition.
Let $V$ be a vector space over $\mathbb{R}$ (or $\mathbb{C}$). A map
$b\colon V \times V \to \mathbb{R}$ is a symmetric bilinear form, if

1. $ b(v,w)=b(w,v) \quad \forall v,w \in V $
2. $ b(\alpha_1 v_1 + \alpha_2 v_2,w) = \alpha_1 b(v_1,w) +
   \alpha_2 b(v_2,w)$ for all $\alpha_1,\alpha_2 \in \mathbb{R}$, $v_1, v_2, w \in V$.

$b$ is non-degenerate, if
\[b(v,w)=0 \quad \forall w \in V \Rightarrow v=0\,.\]
The corresponding quadratic form is defined by
\[q(v)=b(v,v) \quad \forall v \in V\,.\]

The symmetric bilinear form is determined by the corresponding quadratic form:
\begin{align*}
b(v,w)=\frac{1}{2} (q(v+w)-q(v)-q(w))\,.
\end{align*}
If $\{v_1, \dotsc ,v_n \}$ is a basis of V, then we can associate a matrix to a bilinear form by
\[B=(b_{ij})_{i,j=1,\dots,n} \quad \text{with} \quad b_{ij}:=b(v_i,v_j) \,.\]
This yields
\[b(v,w) = b\left(\sum_{i=1}^n x_i v_i \, , \sum_{j=1}^n y_j v_j \right)
= \sum_{i=1}^n \sum_{j=1}^n b(v_i,v_j) x_i y_j
= \sum_{i=1}^n \sum_{j=1}^n b_{ij} x_i y_j = v^T B w\,.
\]

For the quadratic form this implies
\begin{align*}
q(v) = v^T B v = \sum_{i,j=1}^n b_{ij} x_i x_j\,.
\end{align*}

Remark.
Quadratic forms correspond to homogeneous polynomial of degree two.

Theorem of Sylvester
For vector spaces over $\R$, for a given quadratic form $q$ there exists a basis such that
\[q(v)=\sum_{i=1}^p x_i^2 – \sum_{i=p+1}^{p+q} x_i^2\,.\]
Over $\C$ there exists a basis such that
\[q_c(v)=\sum_{i=1}^p z_i^2\,.\]
The triple $(p,q,n-p-q)$ is the signature of the quadratic form $q$. The
signature is invariant wrt. change of basis. $q$ is non-degenerate, if and only if $p+q=n$.

Definition.
If $q$ is a non-zero quadratic form on $\mathbb{R}^3$. Then
\begin{align*}
\phi = \{ \left[ x \right] \in \mathbb{R}P^2 \, | \, q(x)=0 \}
\end{align*}
is a conic.
This definition does not depend on the choice of representative vectors.

Every quadratic form on $\mathbb{R}^3$ corresponds to a symmetric $3\times 3$-matrix.
So it is defined by 6 real values. Every quadratic form corresponds to a point in
$\mathbb{R}^6$. $q$ and $\lambda q$ define the same conic $\phi$, so a conic corresponds
to a point in $\mathbb{R}P^5$. According to the Sylvester Theorem there exists a
basis, such that
\begin{align*}
q(v)=\lambda_1 x_1^2 + \lambda_2 x_2^2 + \lambda_3 x_1^3 \quad
\forall \lambda_i=-1,0,1 \,.
\end{align*}

Non-degenerate conics

1. $ q(v) = x_1^2 + x_2^2 + x_3^2 $, signature (+++)
   $\{ \left[ x \right] \in \mathbb{R}P^2 \, | \, q(x)=0 \}
   = \{ \left[ x \right] \in \mathbb{R}P^2 \, | \, x_1^2+x_2^2=-1 \}
   = \emptyset $
2. $ q(v) = x_1^2 + x_2^2 – x_3^2 $, signaturw (++–)
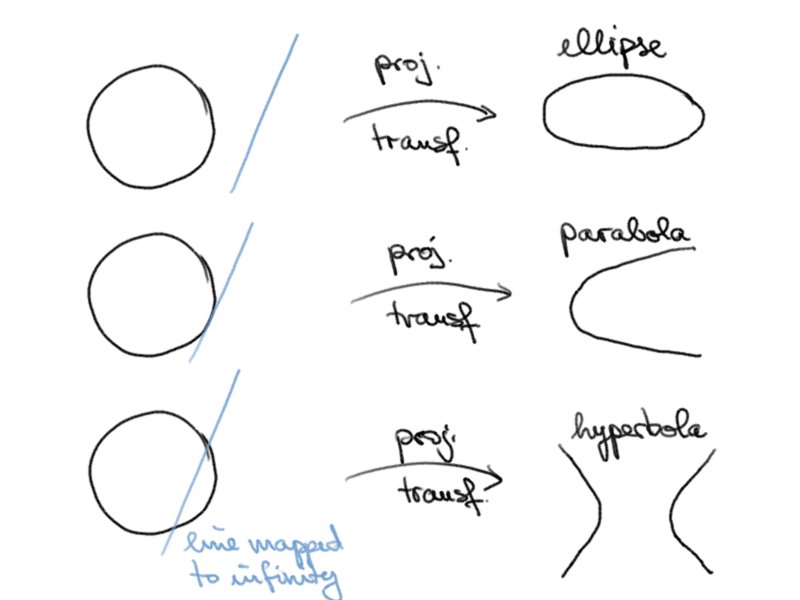
   ellipse, hyperbola, parabola

Degenerate conics

1. $ q(v) = x_1^2 + x_2^2 $, signature (++0) – a point in $\mathbb{R}P^2$
2. $ q(v) = x_1^2 – x_2^2 $, signature (+-0) – two lines in $\mathbb{R}P^2$ ($x_1=x_2$, $x_1=-x_2$)
3. $ q(v) = x_1^2 $, signature (+00) – a point in $\mathbb{R}P^2$

Depending on the affine coordinate we obtain different affine images of the conic
with signature (++-).

Theorem.
Let $P_1$, $P_2$, $P_3$, $P_4$, $P_5 $ be five points in $\mathbb{R}P^2$, then there
exists a conic through $ P_1,\, \dots \, , P_5$. Moreover

1. If no four points lie on a line, the conic is unique.
2. If no three points lie on a line, the conic is non-degenerate.

Lemma.
If three collinear points are on a conic, then the conic contains the whole line.

Proof: Let $P_1=\left[ v_1 \right]$, $P_2=\left[ v_2 \right]$,
$P_3=\left[ v_1+v_2 \right]$ be three collinear points.
\begin{align*}
0=b(v_1,v_1)=q(v_1), 0=q(v_2)=b(v_2,v_2) \qquad ,P_1,P_2 \text{ on conic}\\
0=q(v_1+v_2) = b(v_1+v_2,v_1+v_2) = b(v_1,v_1)+2b(v_1,v_2)+b(v_2,v_2)\\
\Rightarrow b(v_1,v_2)=0\,.
\end{align*}
So for $Q=\left[ sv_1+tv_2 \right]$ we obtain
\begin{align*}
q(sv_1+tv_2)=s^2 b(v_1,v_1) + 2st b(v_1,v_2) + t^2 b(v_2,v_2) = 0
\end{align*}
and $q$ lies on the conic.