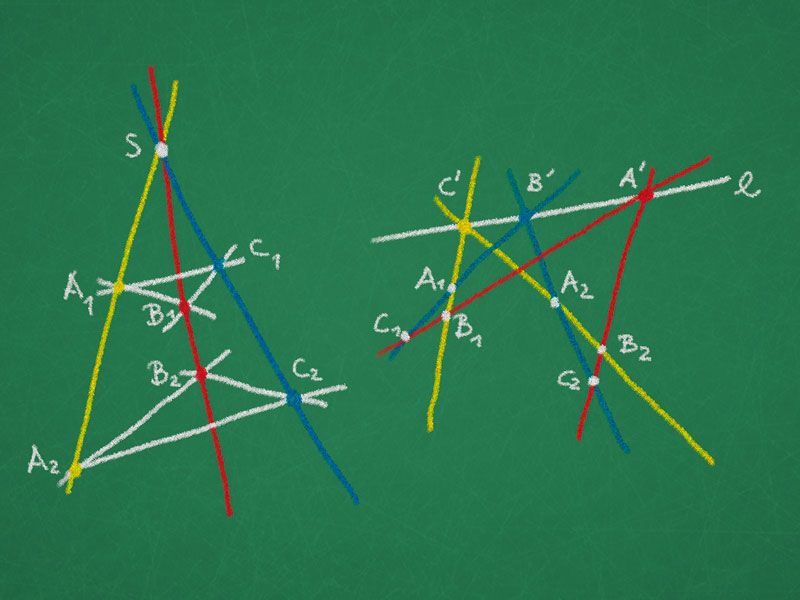
Definition: Two triangles $\triangle_1 = \triangle(A_1, B_1, C_1)$ and $\triangle_2 = \triangle(A_2, B_2, C_2)$ are in perspective w.r.t. a point $S$ if

\[
S = (A_1 A_2) \cap (B_1 B_2) \cap (C_1 C_2)
\]

The triangles are in perspective w.r.t. a line $\ell$ if

\begin{align*}
A’ = (B_1 C_1) \cap (B_2 C_2)\\
B’ = (A_1 C_1) \cap (A_2 C_2)\\
C’ = (A_1 B_1) \cap (A_2 B_2)\\
\end{align*}

lie on $\ell$.

Theorem (Desargues): Let $\triangle_1 = \triangle(A_1, B_1, C_1)$ and $\triangle_2 = \triangle(A_2, B_2, C_2)$ be two triangles. Then $\triangle_1$ and $\triangle_2$ are in perspective w.r.t. a point if and only if they are in perspective w.r.t. a line.

Proof:
$\Rightarrow$: We may assume that $A_1, A_2, S$ and $B_1, B_2, S$ and $C_1, C_2, S$ are in general position on their respective lines. By a Lemma from Lecture 3 we may choose representative vectors

\begin{align*}
A_1 &= \sqvector{a_1}, A_2 = \sqvector{a_2}, S = \sqvector{s} &\text{ such that } a_1+a_2+s=0\\
B_1 &= \sqvector{b_1}, B_2 = \sqvector{b_2} &\text{ such that } b_1+b_2+s=0\\
C_1 &= \sqvector{c_1}, C_2 = \sqvector{c_2} &\text{ such that } c_1+c_2+s=0
\end{align*}

We have: $a_1+a_2=b_1+b_2=c_1+c_2=-s$. The points of intersection of corresponding sides are:

\begin{align*}
(A_1 C_1) \cap (A_2 C_2) &= \sqvector{a_1-c_1} = \sqvector{c_2-a_2}\\
(A_1 B_1) \cap (A_2 B_2) &= \sqvector{b_1-a_1} = \sqvector{a_2-b_2}\\
(B_1 C_1) \cap (B_2 C_2) &= \sqvector{c_1-b_1} = \sqvector{b_2-c_2}
\end{align*}

These three points lie on one line, because

\[
(a_1-c_1)+(b_1-a_1)+(c_1-b_1)=0
\]

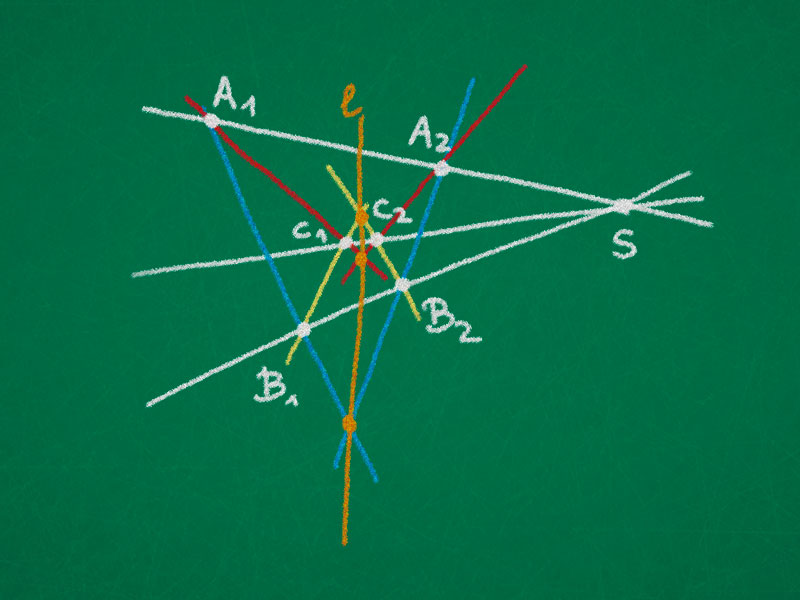
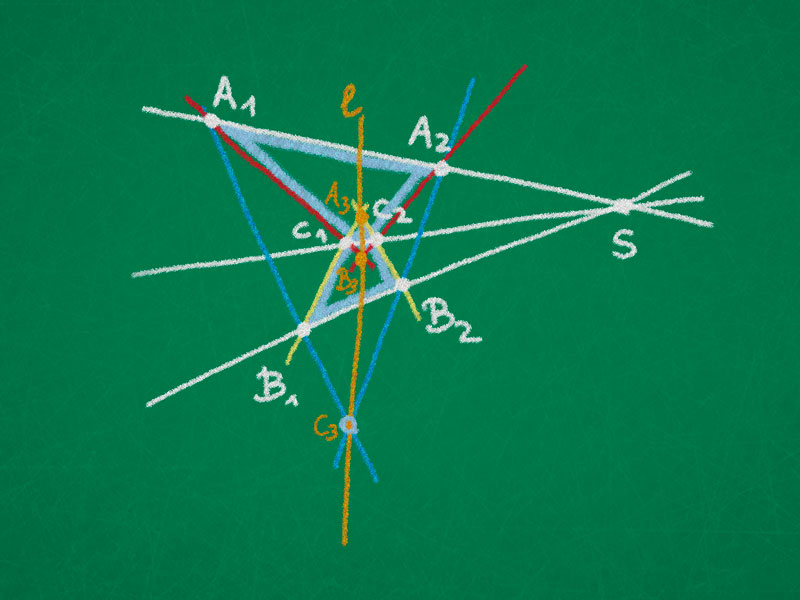
$\Leftarrow$: Starting with triangles $\triangle_1 = \triangle(A_1, B_1, C_1)$ and $\triangle_2 = \triangle(A_2, B_2, C_2)$ in perspective w.r.t. the line $\ell = (A_3 B_3) = (A_3 C_3) = (B_3 C_3)$ we observe that the triangles $\triangle(A_1, A_2, B_3)$ and $\triangle(B_1, B_2, A_3)$ are in perspective w.r.t. $C_3$. Then the forward direction implies that

\begin{align*}
C_1 &= (A_1 B_3) \cap (B_1 A_3) \\
C_2 &= (B_2 A_3) \cap (A_2 B_3) \\
S &= (A_1 A_2) \cap (B_1 B_2)
\end{align*}

are collinear. Hence the triangles $\triangle_1$ and $\triangle_2$ are in perspective w.r.t. $S$.

3d picture:
If we consider two triangles in $\RP^3$ in perspective w.r.t. a point $P$, then each triangle spans a plane and these planes intersect in a line. The intersection points of corresponding sides of the triangles have to lie on the intersection line of the planes. And hence the triangles are in perspective w.r.t. this line.

Symmetry of the Desargues configuration:
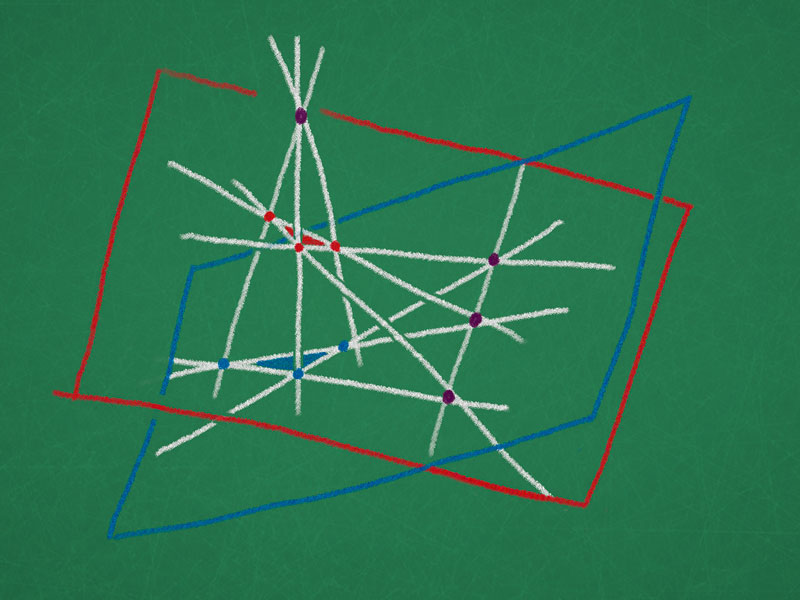
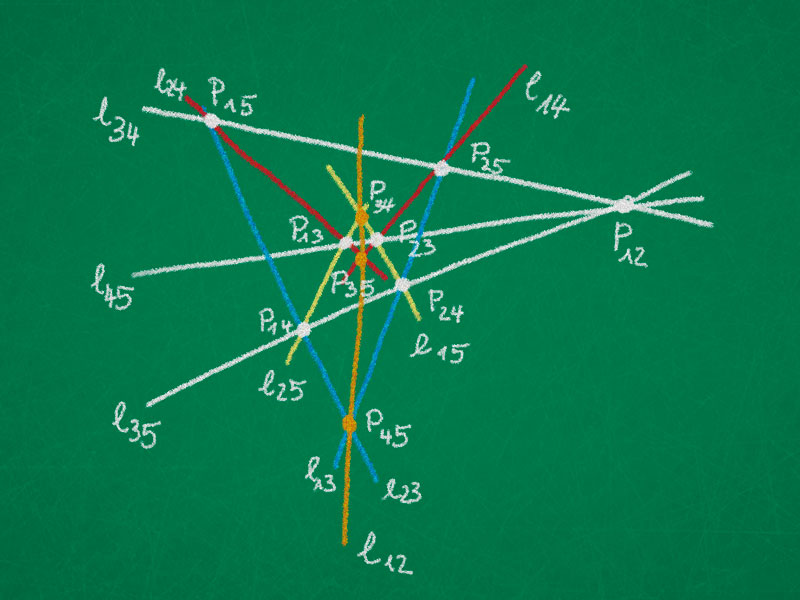
Consider 5 points $A_1, A_2, \dots, A_5$ in $\RP^3$ in general position. Further let $\ell_{ij} = (A_i A_j)$ be the ten lines spanned by these points and let $E_{ijk} = (A_i A_j A_k)$ be the ten planes spanned by these points. Every line is contained in three planes and every plane contains three lines. Now intersect this configuration with a plane $E$ different from $E_{ijk}$ and introduce the following labels:

\begin{align*}
p_{ij} &= \ell_{ij} \cap E\\
g_{ij} &= E_{klm} \cap E \text{ with } \{i, j, k, l, m\} = \{1, 2, 3, 4, 5\}
\end{align*}

This labelling shows that there are $\binom{5}{2}$ pairs of perspective triangles.