Let $x,y,z\in \mathbb{R}$ vertices and the “wrap” $g\in \mathrm{G}$ an edge. Then wie have the vertices head and tail and the edges prev and next.

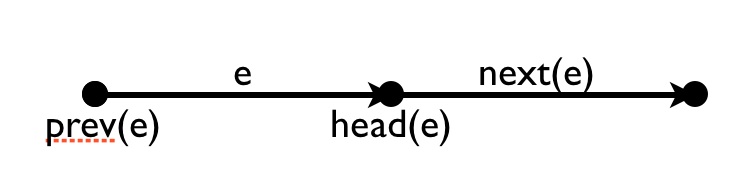
component(e)
mark(e);
e' := e;
while(e'≠ e) do
e' := next(e');
if (e' == e) return true;
mark(e');
endwhile
e':=e;
while (e' ≠ NULL) do
e' := prev(e');
if(e'==e) return false;
mark(e');
endwhile

findcomponents()
num_circles :=0;
num_ints :=0;
unmark all edges;
for each edge e do
if (marked(e)) continue;
if (component(e))
then num_circles ++;
else num_ints++;
endif

Data Structure for surfaces

There are winged edges, half edges and quad edges. An oriented edge has the vertices head and tail and the faces left and right.

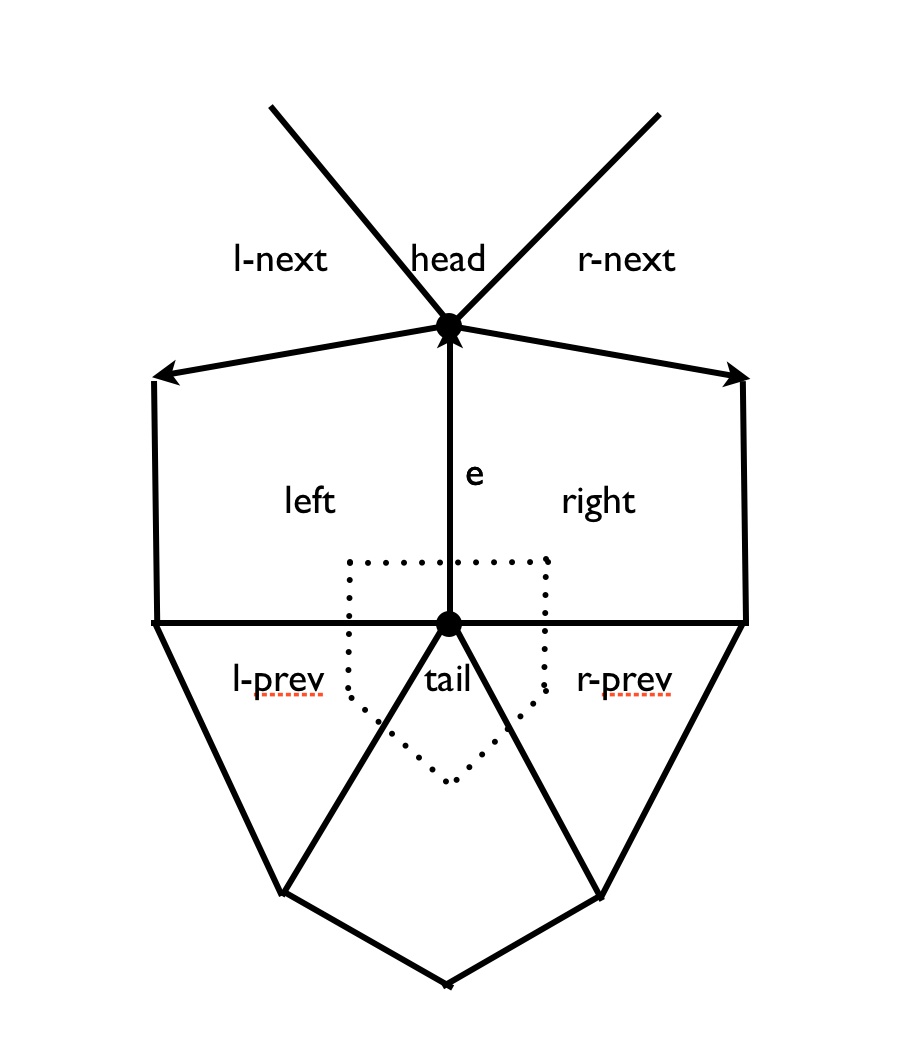
head-next(e) = – r-next(e)
head-prev(e) = – l-next(e)
tail-next(e) = – l-prev(e)
tail-prev(e) = – r-prev(e)

There is a duality: vertex $\leftrightarrow$ face, edge $\leftrightarrow$ edge ($\mathrm{\perp }$) and face $\leftrightarrow$ vertex.
Quad edge represents both together, vertex and face are the same data structure (e.g. coordinates of vertex area of dual face). A “quad edge<2 has pointers to four vertices/faces and pointers to four other quad edges.
Store quad edge once. A reference to a quad edge is a pointer to this data structure together with two bits $\pm e$, $\pm e^{+}$. We need enumerators for each edge, vertex and face. and some pointers back from a vertex/face to an incident edge.

mark all edges, faces, vertices
for each edge e do
if unmarked(e)
then find_component(left(e));
end for


find_component(f)
recursively mark all neighbors (breath-first or order-first, pruning when we see a marked face);
As we go, count faces, edges, vertices;

If we pass a marked face again with oposite direction, set a “nonorientability” flag.

Need to count components: $\chi =\mathrm{V}-\mathrm{E}+\mathrm{F}$.
With some modifications quad edges, etc. also work for multigraphs in a surface.

Similarly, for any 2-complex in ${\mathbb{R}}^3$ or for a 3-manifold given as a 3-complex we can use facet edge data structure.
A facet edge $f_e$ represents one edge of one face in the complex.

next_edge($f_e$), next_facet($f_e$), prev_edge($f_e$), prev_edge($f_e$)

The facet edge has four pointers to $f_e$’s, 2 pointer to vertices (head, tail) and 2 pointers to cells (above, below).
Especially when the complex forms a closed 3-manifold, we can implement duality as quad edge.