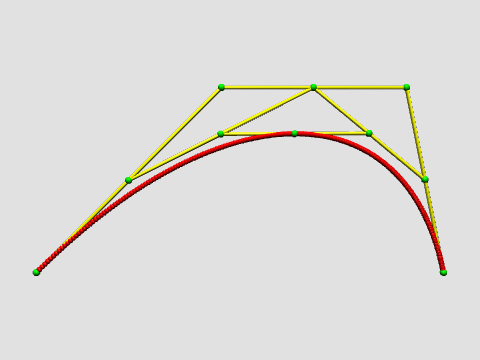
I introduced Bezier curves and surfaces yesterday with a quick and non-technical treatment focusing on the recursive definition of the Bezier curve of order $k$ as a weighted sum of two Bezier curves of order $k-1$; the recursion is rooted in the definition that order-1 Bezier curves are line segments linearly interpolated between a pair of control points:

$$\beta (P_0,P_1;t):=(1-t)P_1+t{P}_2$$

The definition of order-2 (quadratic) Bezier curve is then

$$\beta (P_0,P_1,P_2;t):=(1-t)\beta (P_0,P_1,t)+t\beta (P_1,P_2,t)$$

In general, one arrives at a polynomial expression in terms of the control points $P_i$ which is given for the order-n case by:

$$\sum _{k=0}^n{B}_k^n(t)P_k$$

where $B_k^n(t)$ is the Bernstein polynomial defined by $B_k^n(t):=(\genfrac{}{}{0ex}{}{n}{k})(1-t{)}^k{t}^{n-k}$. Using this form it is not difficult to prove many attractive properties of the Bezier curves, such as: the tangent direction at $P_0$ is in the direction of $P_1$, etc.

To help you visualize the recursive definition of Bezier curves, I’ve created a demo in the SVN repository for our class. Update and run the main() method in util.BezierDemo. You’ll need to invoke the animation panel and set two key frames (by clicking on Save then Insert buttons), then hit the play button.  You’ll probably want to adjust the playback speed also.  Here’s a movie showing the result:

Rational Bezier curves.  If one uses homogeneous coordinates for the points of space, then one can generate a wider variety of curves using the same algorithm.  Remember, the final step of drawing the curve is to dehomogenize, that is, divide by the homogeneous coordinate, which in our case is the $w$-coordinate. Such a curve is then a rational rather than a polynomial curve.

Representation of circles. In particular, it is possible to parametrize arcs of circles using rational Bezier curves of degree 2.  This takes advantage of the fact that the circle an be represented rationally as the homogeneous curve $(1-t^2,2t,1+t^2)$.  For $t\in [0,1]$, this parametrizes the first quadrant of the unit circle.  It turns out that the Bezier curve with control points

$$P0:=(1,0,1),P1:={\displaystyle \frac{\sqrt{2}}{2}}(1,1,1),P2:=(0,1,1)$$

provides essentially the same parametrization of this circular arc.

Bezier surfaces.  There are two approaches to generalizing the above approach to generate surfaces.  In the first, one begins with a triangle instead of a line segment, and two parameters $u$ and $v$ instead of $t$.  Then the order-1 interpolation of the triangle is defined as

$$\beta (P_0,P_1,P_2;u,v):=(1-u-v)P_0+u{P}_1+v{P}_2$$

The other approach creates surfaces as the tensor product of two curves.  In this case, one requires for an order-n surface a total of $(n+1{)}^2$ control points.  One considers these points arranged in a square array.  Then to create the surface, consider each row of the array as the control points for an order-$n$ Bezier curve.  Use the $u$ parameter to obtain a point on each of these curves.  Then, consider these $n+1$ points as the control points of a Bezier curve, and apply the $v$ parameter to obtain a point on it.  This is the value of the surface at the parameter value $(u,v)$.  It’s not hard to show that one obtains the same result if one begins with the $v$ parameter and then applies the $u$.