The norm of an $m\times n$-matrix $A$ is defined as

$\displaystyle ||A||^2 =  \textrm{tr}(A^t A) = \sum_{i,j} a_{ij}^2$.

It stays the same if we multiply $A$ from the left or from the right by an orthogonal matrix $R$:

$||RA||^2 =\textrm{tr}((RA)^t(RA)) =\textrm{tr}(AR^t RA)=||A||^2$

$||AR||^2 = \textrm{tr}((AR)^t(AR)) = \textrm{tr}(R)^{-1} A^t A R))=||A||^2$.

Note that the identity matrix has norm one.

For a a smooth map $f: U \rightarrow \mathbb{R}^m$ from some compact domain $U \subset \mathbb{R}^n$ into $\mathbb{R}^m$ we define the Dirichlet energy of $f$ as

$\displaystyle E(f) := \int_U ||df||^2$.

We think of $U$ as made of some ideal elastic material that wants to contract to a point. The Dirichlet energy is then the elastic energy needed to stretch $U$ via the map $f$ into some given shape. Note that the identity map on $U$ has the volume of $U$ as its Dirichlet energy.

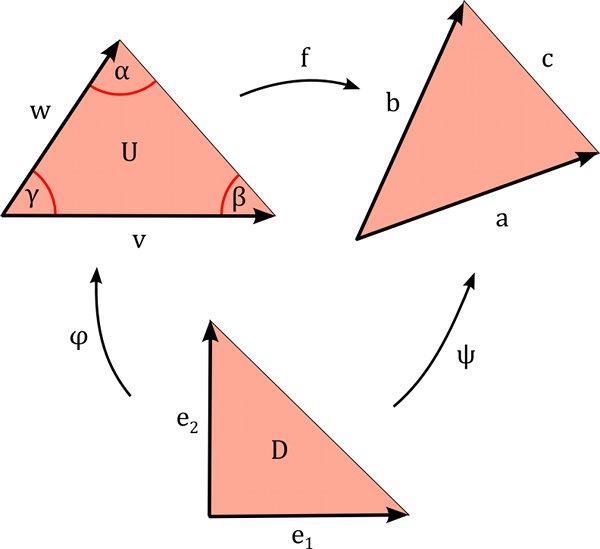
We are interested in the case where $U$ is a triangle in $\mathbb{R}^2$ and $f$ is an affine map. Then $df$ is constant on $U$. Denote by

$D=\{(x,y)\in\mathbb{R}^2 \,|\, 0\leq x,y,1-x-y \}$.

the “standard” triangle in $\mathbb{R}^2$ with edge vectors $e_1,e_2$. Denote by $\varphi$ an affine map that maps $D$ onto $U$. Then $\psi:=f\circ \varphi$ also is an affine map. Define vectors

$v:= d\varphi(e_1)\in \mathbb{R}^2$

$w:= d\varphi(e_2)\in \mathbb{R}^2$

$a:= d\psi(e_1) = df(v) \in \mathbb{R}^m$

$b:= d\psi(e_2)= df(w)\in \mathbb{R}^m$.

Thus we have the following picture:

Then we have

$\displaystyle d\psi^t d\psi = \left( \begin{array}{cc} \langle a,a\rangle & \langle a,b\rangle \\ \langle a,b\rangle &\langle b,b\rangle \end{array} \right)$

$\displaystyle d\varphi^{-1} (d\varphi^{-1})^t  = \frac{1}{4A^2}\left( \begin{array}{rr} \langle w,w \rangle & -\langle v,w \rangle \\ -\langle v,w \rangle &\langle v,v \rangle \end{array} \right)$

where

$\displaystyle A := \frac{\det d\varphi}{2}$

is the area of $U$. From

$df = d\psi \circ d\varphi^{-1}$

we then obtain

$\displaystyle ||df||^2 \\\\=  \textrm{tr} ((d\varphi^{-1})^t d\psi^t d\psi d\varphi^{-1})\\\\=\ \textrm{tr} (d\psi^t d\psi d\varphi^{-1}(d\varphi^{-1})^t)\\\\=\frac{1}{4A^2}(\langle a,a\rangle \langle w,w \rangle-2\langle a,b\rangle\langle v,w \rangle+\langle v,v \rangle\langle b,b\rangle)\\\\=\frac{1}{4A^2}((\langle w,w \rangle-\langle v,w \rangle)|a|^2+(\langle v,v \rangle-\langle v,w \rangle)|b|^2+\langle v,w \rangle|c|^2)\\\\=\frac{1}{4A^2}(\langle w-v,w \rangle |a|^2+\langle v,v-w \rangle|b|^2+\langle v,w \rangle|c|^2)\\\\=\frac{1}{2A}(\cot \alpha \,|a|^2 + \cot \beta \,|b|^2+ \cot \gamma \,|b|^2).$

Here we have used

$c=b-a$

$-2\langle a,b\rangle=|c|^2-|a|^2-|b|^2$

$\displaystyle \cos \gamma = \frac{\langle v,w \rangle}{|v|\,|w|}$

$\displaystyle \sin \gamma = \frac{2A}{|v|\,|w|}$

and similar formulas for $\alpha$ and $\beta$. Thus we arrive at the following

Theorem (cotan formula): For an affine map $f$ between triangles we have

$E(f) = \frac{1}{2}(\cot \alpha\, |a|^2 + \cot \beta\, |b|^2+ \cot \gamma \,|b|^2)$.