Spherical Rectangle with prescribed Length and Area
As Keenan wrote in this post: “To generate a Hopf torus with a prescribed conformal structure, we need to be able to generate a curve on the unit sphere with prescribed length \(L\) and area \(A\).” Unlike Ulrich did in his paper, we decided to focus on a spherical rectangle instead of an “exclusive or” of two disks.
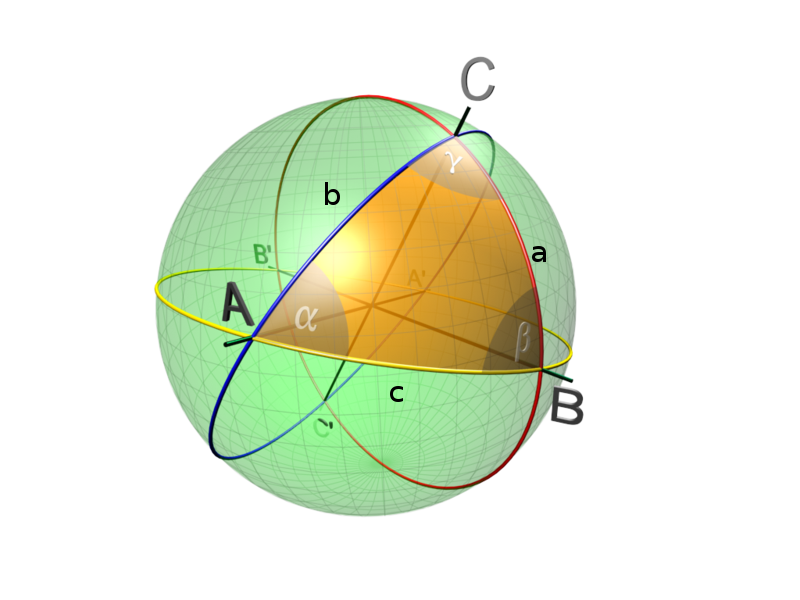
First we should recap some basic spherical trigonometry for Euler triangles. Any spherical triangle has three sides \(a, b, c\) and three opposite angles \(\alpha, \beta\) and \(\gamma \), see Figure below, ( figure-source ):
Of course the sides \(a, b, c\) are basically angles at the origin as well. The definition for a Euler triangle says that any side and any angle of the triangle is smaller than \(\pi\). So the triangle sits on one side of a half-sphere. We get the following equations for area \(A\) and length \(L\):
\[A = \alpha + \beta + \gamma -\pi \\ L = a + b + c \]
We are dealing with unit spheres so we don’t have to care about the radius of the sphere. Further there exist a sinus- law
\[ \frac{\sin a}{ \sin \alpha} = \frac{\sin b}{ \sin \beta} = \frac{\sin c}{ \sin \gamma}, \]
and two co-sinus laws, one for the sides and one for the angles
\[ \cos a = \cos b \cdot cos c + \sin b \cdot \sin c \cdot \cos \alpha \\ \cos \alpha = -\cos \beta \cdot \ cos \gamma + \sin \beta \cdot \sin \gamma \cdot \sin a, \]
similar for the sides \(b, c\) and angles \(\beta, \gamma \). There exist also a bunch of other laws and equations, like \(\tan, \cot,\) half-angle-, half-side -law, and further the equations of Delambre and Napier. All these equations can be checked out at the German wikipedia site , which is surprisingly better than the English one on that point.
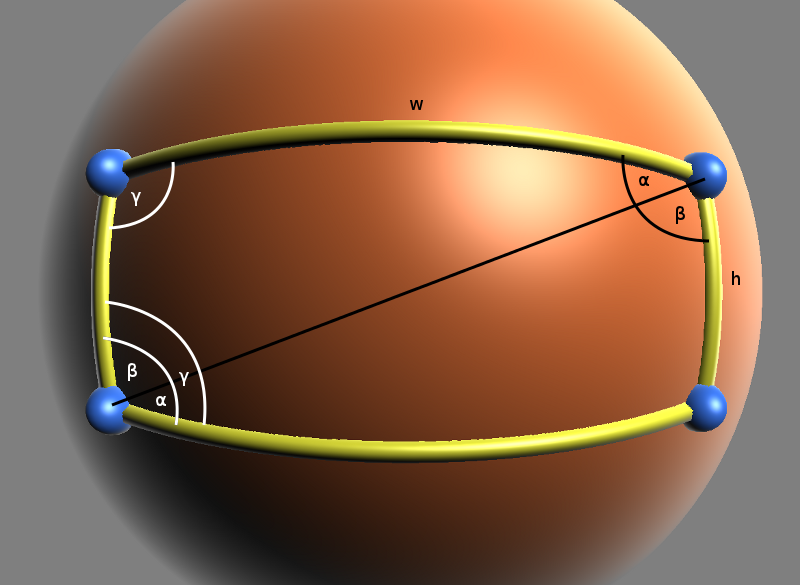
The area and length of a spherical rectangle are
\[A = 2\cdot (\alpha + \beta + \gamma -\pi) \\ L = 2 \cdot (w + h) \]
where \(w=a:=\) width and \(h=b:=\) height
Due to symmetry we know that all four angles have the same size. If we choose \(a, b\) as \(w, h\), all the angles become \(\gamma\). Further we can express \(\gamma\) in terms of \(\alpha\) and \(\beta\) and update the area equation:
\[ \gamma = \alpha + \beta \\ A = 2 \cdot (2 \gamma -\pi) = 4 \gamma -2 \pi \]
We can now solve for \(\gamma \)
\[ \gamma = \frac{A}{4} + \frac{\pi}{2} \]
but still need an expression for the width and height. I tried to find a solution for them in terms of area, circumsphere and the angle \(\gamma\) by playing around with the trigonometrical laws, but couldn’t find any until I had a deeper look at Napier equations and found the solution:
\[ \tan \left( \frac{\alpha + \beta}{2} \right) \cdot \cos \left(\frac{w+h}{2} \right)= \cot \left(\frac{\gamma}{2} \right) \cdot \cos \left(\frac{w-h}{2}\right)\]
We already know that \(\alpha + \beta = \gamma\) and \(w+h = \tfrac{L}{2}\). So we can solve the above equation for
\[ \cos \left(\frac{w-h}{2} \right) \cdot \cot \left(\frac{\gamma}{2} \right)= \tan \left( \frac{\gamma}{2} \right) \cdot \cos \left(\frac{L}{4} \right) \\ \cos \left(\frac{w-h}{2} \right) = \tan^2 \left(\frac{\gamma}{2} \right) \cdot \cos \left(\frac{L}{4} \right) \]
We can solve the length equation for the height \(h \) and put the solution into the \( \tfrac{w-h}{2}\)-equation above
\[h = \tfrac{L}{2} -w \\ \frac{w-h}{2} = \frac{w-(\tfrac{L}{2}-w)}{2} = w-\frac{L}{4} \]
Finally we solve for the width:
\[ \cos \left(w-\frac{L}{4} \right) = \tan^2 \left(\frac{\gamma}{2} \right) \cdot \cos \left(\frac{L}{4} \right) \\ w-\frac{L}{4} = \cos^{-1} \left( \tan^2 \left(\frac{\gamma}{2} \right) \cdot \cos \left(\frac{L}{4} \right) \right) \\ \boxed{w = \cos^{-1}( \tan^2 (\frac{\gamma}{2}) \cdot \cos (\frac{L}{4})) +\frac{L}{4}} \]
And of course we get the height by the equation above \(\boxed{h = \tfrac{L}{2} -w}\). That’s all we need.
I have no clue so far how Napiers equations work out and will focus on that on a different post.
The final question is: Why are we dealing with rectangles instead of triangles, squares or circles, as Ulrich did?
Lets first focus on squares. The expression for the length would be pretty simple and we could directly solve for the four sides \(a\):
\[L = 4 \cdot a \]
However, this would also determine an area \(A’\), which isn’t the same as our prescribed area \(A\), except for some special cases. Therefore, we can’t deal with squares.
Switching to circles, we have an similar problem as for squares. We simply have just one degree of freedom, here the radius \(r\) instead of \(a\) for the four sides of a square. So we are not able to solve it directly with a circle and need some kind of intersecting double/triple-disk construction as Ulrich and Keenan mention in their post/paper above. Another reasonable solution might spherical ellipses, but I haven’t thought much of it yet.
So, now to the last question. Why aren’t we considering triangles? Due to the symmetry condition, we had these nice angle assumptions \(\alpha+\beta=\gamma\) and an easier equation for the circumsphere, so we could easily deal with Napier’s equation. I still haven’t found a solution for the triangle. There is maybe a solution if we fix one angle to \(90\) degrees, which I haven’t calculated yet. Anyway the rectangle seems to be a nice solution and we should stick with it in the mean time.