Let $M$ be a triangulated domain with the functionspace:
\[W_{PL}:=\bigl\{f:M\rightarrow\mathbb{R}\,\bigl\vert\bigr.\,\,\,\left. f\right|_{T_{\sigma}} \mbox{ is affine for all } \sigma \in \Sigma_2 \bigr\}.\]
On the interior of each triangle $T_{\sigma}$ in $M$ the gradient of a function $g \in W$ is well defined and constant. We will derive a nice formula to compute $\left. \mbox{grad}\;g \right|_{T_{\sigma}}$.
Theorem 1: Let $T \subset \mathbb{R}^2$ be a non degenerated triangle with vertices $p_i,p_j,p_k$ and edges $e_i :=p_k-p_j$, $e_j :=p_i-p_k$, $e_k :=p_j-p_i$. For an affine function $g:T\rightarrow \mathbb{R}$ we define $g_i:=g(p_i)$, $g_j:=g(p_j)$, $g_k:=g(p_k)$. Then there holds:
\[\mbox{grad}\, g = \frac{1}{2A}J\bigl( g_i e_i+g_j e_j+ g_k e_k\bigr),\]
where $A:=\frac{1}{2}\mbox{det}(e_i,e_j) = \frac{1}{2} \langle Je_i,e_j \rangle=\frac{1}{2}\langle Je_j,e_k \rangle=\frac{1}{2}\langle Je_k,e_i \rangle,$ denotes the area of $T$ and $J$ the usual $90$ degree rotation in the plan.
Proof: In order to compute $\mbox{grad}\, g$ consider the curve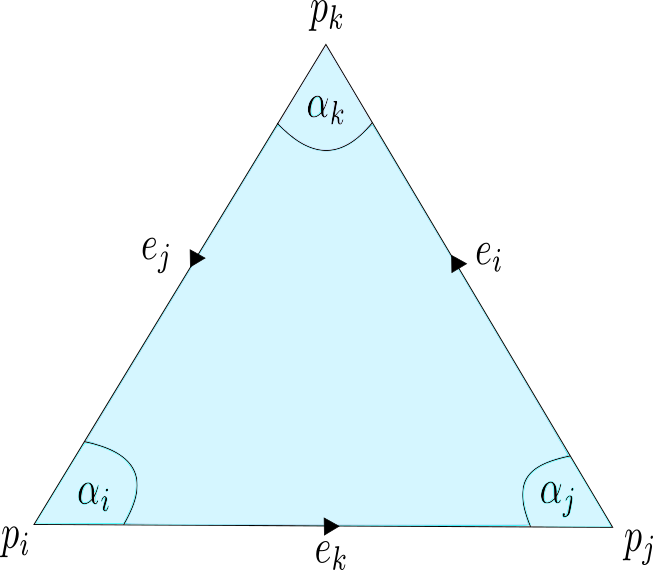
\begin{align*} & \gamma : [0,1] \rightarrow \mathbb{R}^2,\\ & \gamma(t) :=p_j + te_i. \end{align*}
The composition of $g$ and $\gamma$ is given by: $\left( g\circ \gamma\right)(t) = g_j + t\left( g_k – g_j\right)$. Taking the derivative direct and with respect to the product rule we get:
\[g_k -g_j = \left( g\circ \gamma\right)'(t) = g’\left(\gamma(t)\right) \cdot\gamma'(t) = \langle \mbox{grad} \, g, \gamma'(t) \rangle = \langle \mbox{grad} \, g,e_i \rangle. \]
On the other hand we have:
\begin{align*}\bigl\langle\frac{1}{2A}J\left( g_i e_i+g_j e_j+ g_k e_k\right),e_i \bigr\rangle & = \frac{1}{2A} \bigl(g_i \underbrace{\langle Je_i,e_i\rangle }_{=0} + g_j \underbrace{\langle Je_j,e_i\rangle}_{=-2A} + g_k \underbrace{\langle Je_k,e_i\rangle}_{= 2A}\bigr) \\ &= g_k -g_j.\end{align*}
And therfore:
\[\bigl\langle\frac{1}{2A}J\left( g_i e_i+g_j e_j+ g_k e_k\right),e_i \bigr\rangle = \bigl\langle \mbox{grad} \, g,e_i \bigr\rangle.\]
A cyclic permutation of $i,j,k$ gives us:
\[\bigl\langle\frac{1}{2A}J\left( g_i e_i+g_j e_j+ g_k e_k\right),e_j \bigr\rangle = \bigl\langle \mbox{grad} \, g,e_j \bigr\rangle,\]
and we obtain the desired result \[\mbox{grad}\, g = \frac{1}{2A}J\bigl( g_i e_i+g_j e_j+ g_k e_k\bigr).\]
$\square$
Definition: For $g \in W_{PL}$ the Dirichlet energy is defined as:
\[E_D(g) := \frac{1}{2} \int_M \left| \mbox{grad} \, g \right|^2.\]
Theorem 2: We use the same notation as in theorem 1. Additionally let $\alpha_i,\,\alpha_j,\, \alpha_k$ denote the angles of the triangle at the vertices $p_i, \, p_j, \, p_k$ respectively. Then there holds:
\[ \int_T \left| \mbox{grad} \, g \right|^2 = \frac{1}{2}\bigl( \cot (\alpha_i) (g_j-g_k) ^2 + \cot (\alpha_j) (g_k-g_i) ^2 + \cot (\alpha_k) (g_i-g_j) ^2\bigr).\]
Proof: \begin{multline}\int_T \left| \mbox{grad} \, g \right|^2 = \int_T \langle \frac{1}{2A}J\left( g_i e_i+g_j e_j+ g_k e_k\right), \frac{1}{2A}J\left( g_i e_i+g_j e_j+ g_k e_k\right) \rangle \\ =\frac{A}{4 A^2} \Bigl(\Bigr. g_i^2 |e_i|^2 + g_j^2 |e_j|^2 + g_k^2 |e_k|^2 + 2g_ig_j \langle e_i,e_j \rangle + 2g_jg_j \langle e_j,e_k \rangle + 2g_kg_i \langle e_k,e_i \rangle \Bigl)\Bigr.. \end{multline}
On the other hand we have:
\begin{align}\frac{-1}{4A} \bigl(\bigr. \left( g_i -g_j\right)^2 & \langle e_i, e_j \rangle +\left( g_j -g_k\right)^2 \langle e_j, e_k \rangle +\left( g_k -g_i\right)^2 \langle e_k, e_i \rangle \bigl)\bigr. \\ &= \frac{-1}{4A} \bigl(\bigr. g_i^2 \langle e_i,\underbrace{e_j + e_k}_{= – e_i}\rangle -2g_ig_j\langle e_i,e_j \rangle + g_j^2 \langle e_j, \underbrace{e_i + e_k}_{= – e_j}\rangle \\ &\quad\quad\quad -2g_kg_j\langle e_k,e_j \rangle +g_k^2 \langle e_k, \underbrace{e_j + e_i}_{=- e_k}\rangle -2g_ig_k\langle e_i,e_k \rangle \bigl)\bigr. \\ &= \frac{1}{4 A} \bigl(\bigr. g_i^2 |e_i|^2 + g_j^2 |e_j|^2 + g_k^2 |e_k|^2 \\ &\quad\quad\quad+ 2g_ig_j \langle e_i,e_j \rangle + 2g_jg_j \langle e_j,e_k \rangle + 2g_kg_i \langle e_k,e_i \rangle \bigl)\bigr. \\ & = \int_T \left| \mbox{grad} \, g \right|^2.\end{align}
With \begin{align*}\langle e_i,e_j \rangle & = -\cos (\alpha_k) |e_i||e_j|,\\2A = \frac{1}{2}\mbox{det}(e_i,e_j) & = \frac{1}{2} \langle Je_i,e_j \rangle
= \sin(\alpha_k) |e_i||e_j|.\end{align*}
We have:
\[\cot(\alpha_k) = \frac{-\langle e_i,e_j \rangle}{2A}.\]
And therefore we obtain for the Dirichlet energy of $g$ on $T$:
\[ \int_T \left| \mbox{grad} \, g \right|^2 = \frac{1}{2}\bigl( \cot (\alpha_i) (g_j-g_k) ^2 + \cot (\alpha_j) (g_k-g_i) ^2 + \cot (\alpha_k) (g_i-g_j) ^2\bigr).\]
$\square$
Corollary: The Dirichlet energy of $g \in W_{PL}$ is given by :
\[E_D(g) = \frac{1}{4} \sum_{\sigma = \{i,j,k\} \in \Sigma_2} \cot (\alpha_i) (g_j-g_k) ^2 + \cot (\alpha_j) (g_k-g_i) ^2 + \cot (\alpha_k) (g_i-g_j) ^2.\]
If $E:= \left\{ \{i,j\} \in \Sigma\right\}$ denotes the set of edges and $\tilde{E}:= \left\{ (i,j) \in V \times V\, \big \vert \{i,j\} \in \Sigma\right\}$ the set of oriented edges, we choose $\hat{E} \subset \tilde{E}$ such that:
1) $E = \left\{ \{i,j\} \subset V \big \vert (i,j) \in \hat{E}\right\}$,
2) $(i,j) \in \hat{E} \rightarrow (j,i) \notin \hat{E}.$
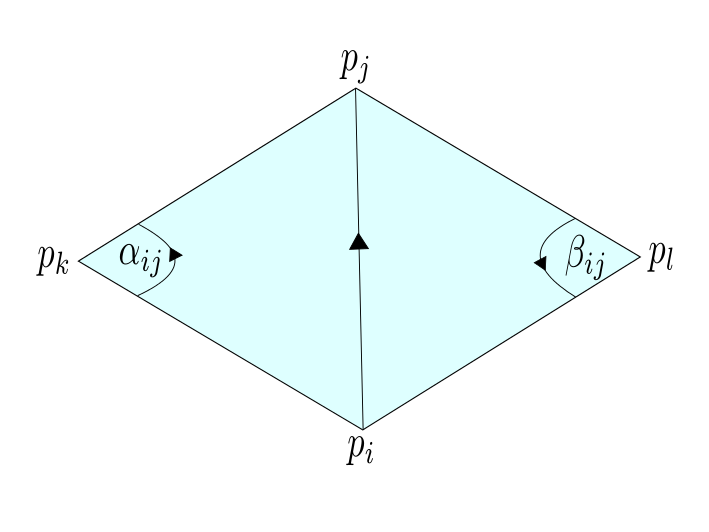
I.e. for every edges we choose oneoriented one. For every $(i,j) \in \hat{E}$ let $\alpha_{ij}$ denote the angle of the opposite vertex to the left and $\beta_{ij}$ the one the opposite vertex to the right. Then we can write the Derichlet energy in the following form:
\[E_D(g) = \frac{1}{4} \sum_{(i,j) \in \hat{E}} \left( \cot(\alpha_{ij}) + \cot{\beta_{ij}}\right) \left(g_i-g_j \right)^2, \]
where we set the cotangent weights zero if the corresponding vertex does not exist because $(i,j)$ is an boundary edge.
