While (for good reasons) we have restricted our treatment of combinatorial cell complexes to the two-dimensional case, the theory of $n$-dimensional simplicial complexes is rather straightforward:
Definition: A simplicial complex is a finite set $P$ together with a set $\mathcal{S}$ of subsets $S\subset P$ with the following properties:
(i) For every $i\in P$ we have $\{i\}\in \mathcal{S}$.
(ii) If $S\in\mathcal{S}$ and $T\subset S,\,T\neq \emptyset$ then $T\in \mathcal{S}$.
An element $S\in\mathcal{S}$ is called a simplex of $\mathcal{S}$ of dimension $k$ if the number of its elements equals $k+1$. The set of all $k$-dimensional simplices in $\mathcal{S}$ is called the $k$-skeleton $\mathcal{S}^k$ of $\mathcal{S}$.
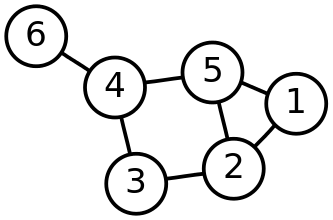
A one-dimensional simplicial complex is the same thing as a graph. The one-dimensional simplices of any simplicial complex are called edges, the two-dimensional simplices are called triangles and the three-dimensional ones are called tetrahedra. The picture below shows a graph with $P=\{1,2,3,4,5,6\}$ and seven edges.
A one-dimensional simplicial complex $\mathcal{S}$ (a graph) can be viewed as a special one-dimensional cell complex $M$ (i.e. a special multigraph). The oriented edges of $M$ is the set of ordered pairs $(i,j)$ with $\{i,j\}\in \mathcal{S}^1$ and the maps $s,d,\rho$ are defined by
\begin{align*}s((i,j))&:=i\\ d((i,j))&:=j \\ \rho((i,j))&:=(j,i).\end{align*}
Similarly, a two-dimensional simplicial complex can be viewed as a special two-dimensional cell complex. The cell-complex below from the last post arises in this way from a two-dimensional simplicial complex with five points, ten edges and six triangles.

We have not really discussed this, but a two-dimensional cell complex describes a unique topological space. The same holds for general simplicial complexes. However, simplicial complexes are much more powerful for the discrete modeling of physical objects for the following reason: The topological space described by a combinatorial simplicial complex comes with a canonical piecewise affine structure. We now elaborate what this means.
Let $\mathcal{S}$ be a simplicial complex with point set $P$. Define then the piecewise affine space $C(\mathcal{S})$ corresponding to $\mathcal{S}$ as the set of all functions $f:P\to \mathbb{R}$ such that $f(i)\geq 0$ for all $i\in P$,
$$\sum_{i\in P}\, f(i)=1$$
and
$$\big\{ \,i\in P \,\,\,\big|\,\,\, f(i)\neq 0\,\big\} \in \mathcal{S}.$$
For each simplex $S\in \mathcal{S}$ we define an affine space
$$\mathcal{A}_S:= \bigg\{\, g: P\to \mathbb{R} \,\,\,\bigg|\,\,\,\sum_{i\in P} g(i)=1\mbox{ and }i\notin S \implies g(i)=0 \,\bigg\}$$
The vector space corresponding to the affine space $\mathcal{A}_S$ is
$$V_S:= \bigg\{\, g: P\to \mathbb{R} \,\,\,\bigg|\,\,\,\sum_{p\in P} g(i)=0\mbox{ and }i\notin S \implies g(i)=0 \,\bigg\}$$
and each $\mathcal{A}_S$ is spanned by the simplex
$$\Sigma_S:=\big\{\, g\in\mathcal{A}_{S} \,\,\,\big|\,\,\,g(i)\geq 0 \mbox{ for all } i\in P \,\big\}.$$
The whole space $C(\mathcal{S})$ is the disjoined union of all the interiors (within $\mathcal{A}_S$) of the simplices $\Sigma_S$ for $S\in \mathcal{S}$. If $S\in \mathcal{S}$ and $T\subset S$ then $\mathcal{A}_T$ is an affine subspace of $\mathcal{A}_S$. Similarly, we also have $\Sigma_T \subset \Sigma_S$ in this case.
Each point $i\in P$ corresponds to a particular element $\delta_i\in C(\mathcal{S})$ defined by $\delta_i(j)=1$ for $j=i$ and $\delta_i(j)=0$ otherwise. We have $\mathcal{A}_{\{p\}}=\Sigma_{\{i\}}=\{\delta_i\}$. The main property that makes simplicial complexes useful for physical modeling is the following easy-to-prove
Theorem: Let $\mathcal{S}$ be a simplicial complex with point set $P$ and let $f: P \to V$ be a map into any vector space $V$. Then there is a unique map
$$\hat{f}:C(\mathcal{S})\to V$$
whose restriction to each simplex $\Sigma_S$ is affine and which extends $f$ in the sense that for all $i\in P$ we have
$$\hat{f}(\delta_i)=f(i).$$
In particular, if we have a two-dimensional simplicial complex and are given a position in $\mathbb{R}^3$ for each of its points, it is clear how to fill in the triangles, for example in order to render them.
