A ruled surface is a surface in \(\mathbb R^3\) that arises from a 1-parameter family of straight lines, i.e. these surfaces are obtained by moving a straight line though the Euclidean space. E.g. a normal vector field of a curve defines such a rule surface:
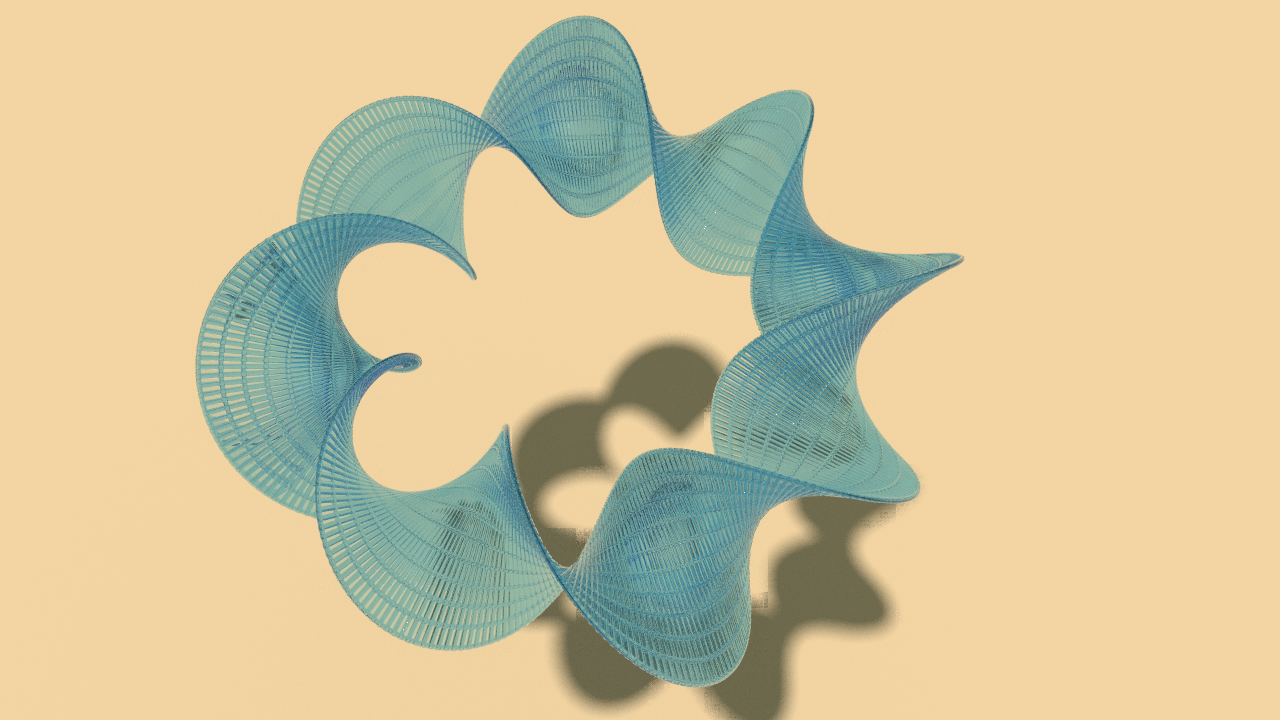
The plane is a ruled surface which – like a soap film – locally minimizes the area, a so called minimal surface. Another, more interesting, ruled minimal surface is the catenoid. Not counting the plane it was the first minimal surface which was discovered and it turns out that with the plane it is the the only rotationally symmetric minimal surface.

Like all minimal surfaces the catenoid comes with a whole 1-parameter family of minimal surfaces – the so called associate family – also containing the helicoid which arises as the skew motion of a straight line along a fixed perpendicular straight line.
The whole family has a closed form expression: For each \(\alpha\in(-\pi,\pi]\) a conformal parametrization is given by\[f\colon (-\pi,\pi]\times\mathbb R \to \mathbb R^3, \quad (x,y) \mapsto \begin{pmatrix}\cos\alpha\,\sinh y\, \sin x + \sin\alpha\, \cosh y\, \cos x \\ -\cos\alpha\,\sinh y\, \cos x + \sin\alpha\, \cosh y\, \sin x \\ x\,\cos \alpha + y\sin\alpha\end{pmatrix}.\]
Exercise: Build a network that visualizes the associated family of the catenoid.
The helicoid construction provides minimal surfaces in hyperbolic 3-space. In this tutorial these hyperbolic helicoids shall be visualized.
We start with the Poincaré half space model of the hyperbolic 3-space: Here the hyperbolic space is represented by the upper half plane \(\mathrm H^3 = \{(x,y,z)\in\mathbb R^3\mid z>0\}\). Though the angles stay the same, distances in \(\mathrm H^3\) are measured differently from the Euclidean half space.
With this notion of distance the hyperplane \(\mathrm E=\{(x,y,z)\in\mathbb R^3\mid z = 0\}\) has infinite distance to each point of \(\mathrm H^3\) and the shortest path between two points is realized by arcs of circles perpendicular to \(\mathrm E\):
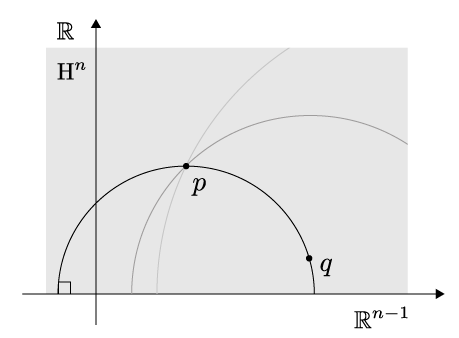
Such locally shortest paths are called geodesics and are the equivalent of straight lines in non-Euclidean geometry. In Euclidean space a helicoid is a straight line, i.e. a geodesic, which rotates with a constant speed while moving on another perpendicular straight line. So in analogy to Euclidean case the hyperbolic helicoids appear by rotating a geodesic (circle perpendicular to \(\mathrm E\)) with constant speed while moving along another geodesic.
This might sound complicated first. Though, the isometries of hyperbolic space turn out to be exactly the Möbius transformations preserving the hyperplane \(\mathrm E\) and any two geodesics can be mapped onto each other by such a Möbius transformation. This allows us to fix the geodesic we move along to be the \(z\)-axis and drastically simplifies the setup: The distance between two points \(p,q\in\mathrm H^3\) that lie on the \(z\)-axis is given just as follows\[d(p,q) = |\ln b\, -\, \ln a\,|,\quad p=(0,0,a),\,q=(0,0,b).\]With this we can construct all hyperbolic helicoids as follows: Let \(\tau\in \mathbb R\) and \(\mathbf v \in \mathrm E\) be of unit length with respect to the standard product of \(\mathbb R^3\), then a parametrization of the hyperbolic helicoid is given by\[f\colon \mathbb R\times(-\tfrac{\pi}{2},\tfrac{\pi}{2}) \to \mathbb R^3,\quad (x,y) \mapsto \cos y\, \Bigl(\begin{smallmatrix}0\\0\\e^x\end{smallmatrix}\Bigr) +\sin y\,e^x\,\Bigl(\cos(\tau x)\,\mathbf v + \sin(\tau x)\,e_3\times \mathbf v\Bigr).\]Here, as usual, \(e_3\) denotes the third basis vector of the standard basis of \(\mathbb R^3\): \(e_3 = (0,0,1)\). All other hyperbolic helicoids are obtained then by postcomposition with Möbius transformations that leave \(\mathrm E\) invariant.

For this particular rendering we equipped the ground with the default clay material and changed its color to a deep blue. The helicoid itself was thickened by a polyextrude node and equipped with whiteporcelain material the color of which we changed to orange. For the light we used the arealight.
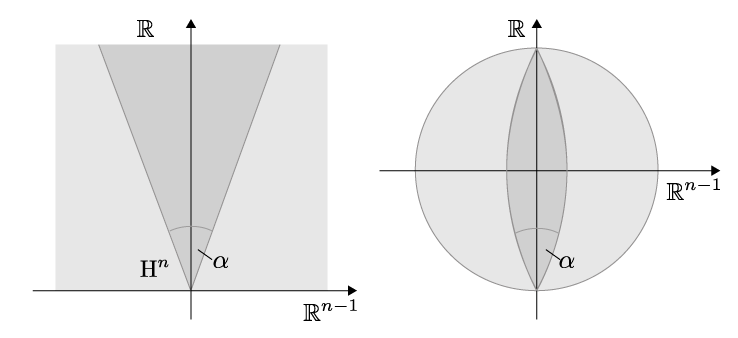
Most of the geometry is hidden in this view. Thus it might be better restrict the map \(f\) to \([-\alpha,\alpha]\times \mathbb R\) for \(0<\alpha<\pi\). This amounts to restricting the image to a cone.

An even better visualization can be achieved by mapping the upper half-plane by a Möbius transformation to unit ball. This map can be achieved by a combining translations and an inversion \(T\) in the unit sphere: First we shift the half space up by adding \(e_3\). If we then apply \(T\) it is mapped to a sphere of radius \(\tfrac{1}{2}\) with center \((0,0,\tfrac{1}{2})\).
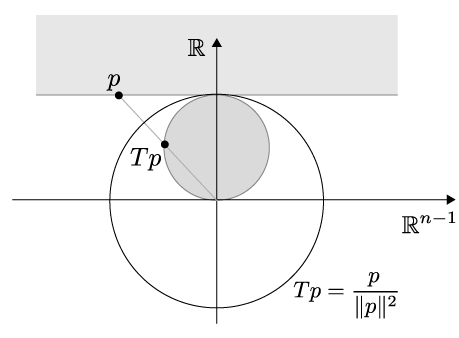
Rescaling by \(2\) and subtracting \(e_3\) yields then a Möbius transformation that sends the upper half plane to the ball of radius \(1\). Altogether the map is given by\[x\mapsto 2\frac{x+e_3\,}{\Vert x+e_3\Vert^2}-e_3.\]Actually by this transformation we get another model of the hyperbolic space known a the Poincaré disk model.
The ball itself can be nicely incorporated in the picture by drawing a unit sphere, which is equipped with the glass material.

Since Möbius transformations are conformal the angles are preserved under this transformation. Further circles (or straight line) are mapped to circles (or straight lines). Thus the straight lines in the cone are mapped to circles all passing through to points on the boundary of the disk – the images of \(0\) and \(\infty\) under the Möbius transformation. Thus the helicoid is bounded by a spindle like surface.

Homework (due 24/26 May): Visualize the hyperbolic helicoids, i.e. implement the construction described above which yields a helicoid that connects the south to the north pole. Use a Möbius transformation to obtain a helicoid that connects the south pole with an arbitrary given point on the 2-sphere.

